题目内容
如图，已知直角三角形ABC，CD是斜边AB上的高，那么下列各关系式：①CD2=AD•BD；②AC•BC=CD•AB；③AC2=AD•AB；④CD≤| 1 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
分析：首先由直角三角形ABC，CD是斜边AB上的高，根据有两角对应相等的三角形相似，即可证得△ACD∽△ABC，△BCD∽△BAC与△ACD∽△CBD，根据相似三角形的对应边成比例，即可证得①②③正确，又由直角三角形斜边上的中线等于斜边的一半与直角三角形的三边关系，即可求得④正确．
解答：解：∵直角三角形ABC，CD是斜边AB上的高，
∴∠ADC=∠ABC=90°，
∵∠C=∠C，
∴△ACD∽△ABC，
∴
=
，
∴AC2=AD•AB，故③正确；
同理：△BCD∽△BAC，
∴
=
，∠DCB=∠A，
∴AC•BC=CD•AB，故②正确；
∵∠ADC=∠BDC=90°，
∴△ACD∽△CBD，
∴
=
，
∴CD2=AD•BD，故①正确；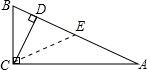
取AB的中点E，连接CE，
则CE=
AB，
∵CE是Rt△CDE的斜边，
∴CD＜CE，
当AC=BC时，CD=CE，
∴CD≤CE≤
AB，故④正确．
故选D．
∴∠ADC=∠ABC=90°，
∵∠C=∠C，
∴△ACD∽△ABC，
∴
| AC |
| AB |
| AD |
| AC |
∴AC2=AD•AB，故③正确；
同理：△BCD∽△BAC，
∴
| AC |
| CD |
| AB |
| BC |
∴AC•BC=CD•AB，故②正确；
∵∠ADC=∠BDC=90°，
∴△ACD∽△CBD，
∴
| AD |
| CD |
| CD |
| BD |
∴CD2=AD•BD，故①正确；
取AB的中点E，连接CE，
则CE=
| 1 |
| 2 |
∵CE是Rt△CDE的斜边，
∴CD＜CE，
当AC=BC时，CD=CE，
∴CD≤CE≤
| 1 |
| 2 |
故选D．
点评：此题考查了相似三角形的判定与性质，以及直角三角形的性质．此题综合性较强，难度适中，解题的关键是注意数形结合思想的应用．
练习册系列答案
计算高手系列答案
相关题目
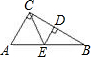如图，已知直角三角形ABC中，∠ACB=90°，E为AB上一点，且CE=EB，ED⊥CB于D，则下列结论中不一定成立的是（ ）| A、AE=BE | ||
B、CE=
| ||
| C、∠CEB=2∠A | ||
D、AC=
|
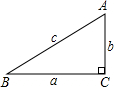如图，已知直角三角形ABC的三边分别为a、b、c，则sinA等于（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
（2012•上城区二模）如图，已知直角三角形OAB的直角边OA在x轴上，双曲线y=
如图，已知直角三角形ABC的周长为