题目内容
 如图,已知梯形ABCD中,AD∥BC,AB=CD=AD,AC、BD相交于O点,∠BCD=60°,下列有6个结论:
如图,已知梯形ABCD中,AD∥BC,AB=CD=AD,AC、BD相交于O点,∠BCD=60°,下列有6个结论:
①梯形ABCD是轴对称图形,②梯形ABCD是中心对称图形,③AC=BD,④BC=2AD,⑤AC⊥BD,⑥AC平分∠DCB
其中正确的有
- A.2个
- B.3个
- C.4个
- D.5个
C
分析:根据等腰梯形的性质对各个结论进行分析,从而判断正确的个数.
解答: 解:①符合等腰梯形的性质,故此结论正确;
解:①符合等腰梯形的性质,故此结论正确;
②等腰梯形是轴对称图形而非中心对称图形,故此结论不正确;
③等腰梯形的对角线相等,故此结论正确;
④过点D作DE⊥BC,过点A作AF⊥BC,则四边形AFED是矩形,
∵∠BCD=60°,
∴∠EDC=30°,
∴CE=BF= CD,
CD,
∵AB=CD=AD,
∴BC=2AD,
故此结论正确;
⑤∵CD=AD,
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠DCA=∠ACB,
∵∠BCD=60°,
∴∠DCA=∠ACB=30°,
∴∠DBC=30°,
∴∠BOC=120°,
故此结论不正确;
⑥∵CD=AD,
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠DCA=∠ACB,
∴AC平分∠DCB,
故此结论正确.
所以正确的是①③④⑥.
故选C.
点评:此题主要考查等腰梯形的性质:①等腰梯形是轴对称图形,它的对称轴是经过上下底的中点的直线;
②等腰梯形同一底上的两个角相等;
③等腰梯形的两条对角线相等.
分析:根据等腰梯形的性质对各个结论进行分析,从而判断正确的个数.
解答:
 解:①符合等腰梯形的性质,故此结论正确;
解:①符合等腰梯形的性质,故此结论正确;②等腰梯形是轴对称图形而非中心对称图形,故此结论不正确;
③等腰梯形的对角线相等,故此结论正确;
④过点D作DE⊥BC,过点A作AF⊥BC,则四边形AFED是矩形,
∵∠BCD=60°,
∴∠EDC=30°,
∴CE=BF=
 CD,
CD,∵AB=CD=AD,
∴BC=2AD,
故此结论正确;
⑤∵CD=AD,
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠DCA=∠ACB,
∵∠BCD=60°,
∴∠DCA=∠ACB=30°,
∴∠DBC=30°,
∴∠BOC=120°,
故此结论不正确;
⑥∵CD=AD,
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠DCA=∠ACB,
∴AC平分∠DCB,
故此结论正确.
所以正确的是①③④⑥.
故选C.
点评:此题主要考查等腰梯形的性质:①等腰梯形是轴对称图形,它的对称轴是经过上下底的中点的直线;
②等腰梯形同一底上的两个角相等;
③等腰梯形的两条对角线相等.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 9、如图,已知梯形ABCD中,AD∥BC,BE平分∠ABC,BE⊥CD,∠A=110°,AD=3,AB=5,则BC的长为( )
9、如图,已知梯形ABCD中,AD∥BC,BE平分∠ABC,BE⊥CD,∠A=110°,AD=3,AB=5,则BC的长为( )
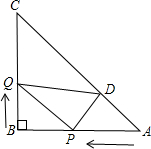 点到达终点时,另一点也随之停止.过Q作QD∥AB交AC于点D,连接PD,设运动时间为t秒时,四边形BQDP的面积为s.
点到达终点时,另一点也随之停止.过Q作QD∥AB交AC于点D,连接PD,设运动时间为t秒时,四边形BQDP的面积为s. (2007•遂宁)如图,已知等腰△ABC的面积为4cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为
(2007•遂宁)如图,已知等腰△ABC的面积为4cm2,点D、E分别是AB、AC边的中点,则梯形DBCE的面积为