题目内容
如图，已知：点A，B、C、D在同一条直线上，CE∥DF，AE∥BF，且AE=BF．求证：AC=BD．
证明：∵CE∥DF，
∴∠ECA=∠FDB．
∵AE∥BF，
∴∠FBD=∠EAC．
又∵AE=BF，
在△AEC与△BFD中，
∴△AEC≌△BFD（AAS）．
∴AC=BD．
分析：解决此题先要证明△AEC≌△BFD，就可得出结论．
点评：本题考查了全等三角形的判定和性质；解决此类问题，首先要根据全等三角形的判定，证明三角形全等，然后得出结论．
∴∠ECA=∠FDB．
∵AE∥BF，
∴∠FBD=∠EAC．
又∵AE=BF，
在△AEC与△BFD中，
∴△AEC≌△BFD（AAS）．
∴AC=BD．
分析：解决此题先要证明△AEC≌△BFD，就可得出结论．
点评：本题考查了全等三角形的判定和性质；解决此类问题，首先要根据全等三角形的判定，证明三角形全等，然后得出结论．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
27、如图，已知P点是∠AOB平分线上一点，PC⊥OA，PD⊥OB，垂足为C、D，
20、如图，已知：点B、D、C、F在一条直线上，且BD=FC，AB=EF，AB∥EF；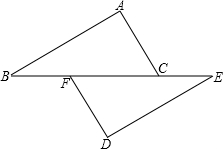
（2012•德化县一模）如图，已知：点B、F、C、E在一条直线上，FB=CE，AC=DF．能否由上面的已知条件证明AB∥ED？如果能，请给出证明；如果不能，请从①AB=ED；②BC=EF；③∠ACB=∠DFE．三个条件中选择一个合适的，添加到已知条件中，使AB∥ED成立，并给出证明．
如图，已知A点坐标为（5，0），直线y=x+b（b＞0）与y轴交于点B，连接AB，∠α=75°，则b的值为