题目内容
 有一直径为
有一直径为| 2 |
(1)求被剪掉的阴影部分的面积;
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
(3)求圆锥的全面积.
分析:(1)因为扇形ABC的圆心角是90°,所以BC为⊙O的直径=
m,△ABC是等腰直角三角形,利用勾股定理即可求出AB即扇形ABC的半径,然后利用扇形面积=
,再求出圆的面积即可求出答案;
(2)利用扇形的底面圆的周长=展开图的弧长即可求解;
(3)利用(2)的所求,圆锥的全面积=展开图中扇形的面积+底面圆的面积.
| 2 |
| nπr2 |
| 360 |
(2)利用扇形的底面圆的周长=展开图的弧长即可求解;
(3)利用(2)的所求,圆锥的全面积=展开图中扇形的面积+底面圆的面积.
解答: 解:(1)连接BC,∵∠A=90°,
解:(1)连接BC,∵∠A=90°,
∴BC为⊙O的直径.
在Rt△ABC中,AB=AC,且AB2+AC2=BC2,
∴AB=AC=1,
∴S阴影=S⊙O-S扇形ABC=π•(
)2-
=
π-
π=
π(m2);
(2)设圆锥底面半径为r,则
长为2πr.
∴
=2πr,
∴r=
(m);
(3)S全=S侧+S底=S扇形ABC+S圆=
π+(
)2•π=
πm2.
 解:(1)连接BC,∵∠A=90°,
解:(1)连接BC,∵∠A=90°,∴BC为⊙O的直径.
在Rt△ABC中,AB=AC,且AB2+AC2=BC2,
∴AB=AC=1,
∴S阴影=S⊙O-S扇形ABC=π•(
| ||
| 2 |
| 90π×12 |
| 360 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
(2)设圆锥底面半径为r,则
 |
| BC |
∴
| 90π×1 |
| 180 |
∴r=
| 1 |
| 4 |
(3)S全=S侧+S底=S扇形ABC+S圆=
| 1 |
| 4 |
| 1 |
| 4 |
| 5 |
| 16 |
点评:本题需灵活掌握扇形的面积公式,结合勾股定理即可解决问题.

练习册系列答案
相关题目
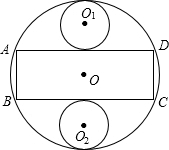 现有一块块直径为2m的圆形铁片,若它做成一个有盖的油桶,并尽可能的用好这块铁片,工人师傅在圆形铁片上截取两个圆(即两底)和一个矩形(侧面),如图.
现有一块块直径为2m的圆形铁片,若它做成一个有盖的油桶,并尽可能的用好这块铁片,工人师傅在圆形铁片上截取两个圆(即两底)和一个矩形(侧面),如图. 现有一块块直径为2m的圆形铁片,若它做成一个有盖的油桶,并尽可能的用好这块铁片,工人师傅在圆形铁片上截取两个圆(即两底)和一个矩形(侧面),如图.
现有一块块直径为2m的圆形铁片,若它做成一个有盖的油桶,并尽可能的用好这块铁片,工人师傅在圆形铁片上截取两个圆(即两底)和一个矩形(侧面),如图.
 )
)