题目内容
以下有两道题,请你选择一道题作答。
(1)已知 ,试确定|a|﹣|b|+|a+b|+|ab|的值;
,试确定|a|﹣|b|+|a+b|+|ab|的值;
(2)如果a,b,c,d为互不相等的有理数,且|a﹣c|=|b﹣c|=|d﹣b|=1,试确定|a﹣d|的值。
(1)已知
 ,试确定|a|﹣|b|+|a+b|+|ab|的值;
,试确定|a|﹣|b|+|a+b|+|ab|的值;(2)如果a,b,c,d为互不相等的有理数,且|a﹣c|=|b﹣c|=|d﹣b|=1,试确定|a﹣d|的值。
解:(1)∵ ,
,
∴a,b同号,
又∵a<﹣b,即a+b<0,
∴a,b必须同为负,
∴|a|﹣|b|+|a+b|+|ab|
=﹣a﹣(﹣b)﹣(a+b)+ab
=﹣2a+ab;
(2)已知b≠c,可设b<c,
∵|a﹣c|=|b﹣c|,
∴a﹣c与b﹣c必互为相反数(否则a=b,不合题意),
即a﹣c=﹣(b﹣c),a+b=2c,
又∵b<c,
∴a>c,
∵|b﹣c|=|d﹣b|,
∴b﹣c与d﹣b必相等(否则c=d,不合题意),
即b﹣c=d﹣b,从而得2b=c+d,
∵b<c,
∴b>d,即d<b<c<a,
∴|a﹣d|=a﹣d=(a﹣c)+(c﹣b)+(b﹣d)=1+1+1=3,
若设b>c,同理可得|a﹣d|=3。
 ,
,∴a,b同号,
又∵a<﹣b,即a+b<0,
∴a,b必须同为负,
∴|a|﹣|b|+|a+b|+|ab|
=﹣a﹣(﹣b)﹣(a+b)+ab
=﹣2a+ab;
(2)已知b≠c,可设b<c,
∵|a﹣c|=|b﹣c|,
∴a﹣c与b﹣c必互为相反数(否则a=b,不合题意),
即a﹣c=﹣(b﹣c),a+b=2c,
又∵b<c,
∴a>c,
∵|b﹣c|=|d﹣b|,
∴b﹣c与d﹣b必相等(否则c=d,不合题意),
即b﹣c=d﹣b,从而得2b=c+d,
∵b<c,
∴b>d,即d<b<c<a,
∴|a﹣d|=a﹣d=(a﹣c)+(c﹣b)+(b﹣d)=1+1+1=3,
若设b>c,同理可得|a﹣d|=3。

练习册系列答案
相关题目
 本题中有两小题,请你任选一题作答.
本题中有两小题,请你任选一题作答.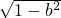 +b
+b =1,则a2+b2=________.
=1,则a2+b2=________. ,试确定|a|-|b|+|a+b|+|ab|的值.
,试确定|a|-|b|+|a+b|+|ab|的值.