Question

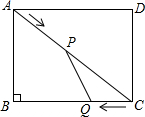如图，在矩形ABCD中，AB=6m，BC=8m，动点P以2m/s的速度从点A出发，沿AC向点C移动，同时动点Q为lm/s的速度从点C出发，沿CB向点B移动，设P、Q两点分别移动ts（0＜t＜5）后，P点到BC的距离为dm，四边形ABQP的面积为S㎡
（1）求距离d关于时间t的函数关系式；
（2）求面积S关于时间t的函数关系式；
（3＞在P、Q两点移动的过程中，四边形ABQP的面积能否是△CPQ面积的3倍？若能，求出此时点P的位置；若不能，请说明理由．

Answer 1

分析：（1）过点P作PE⊥BC于E，利用勾股定理求出AC的长，AP=2t，CQ=t，则PC=10-2t，又PE∥AB，根据平行线分线段成比例列出比例式，继而代入求解即可；
（2）根据S=S_△ABC-S_△PQC，直接计算即可；
（3）假设四边形ABQP的面积是△CPQ面积的3倍，则有：

3

5

t2-3t+24=18，通过判断方程无解，继而得出结论．

解答：解：（1）过点P作PE⊥BC于E，Rt△ABC中，AC=

AB2+BC2

=10（m）
由题意知：AP=2t，CQ=t，则PC=10-2t．                          …（1分）
由AB⊥BC，PE⊥BC，得PE∥AB，
∴

PE

AB

=

PC

AC

，即

PE

6

=

10-2t

10

…（2分）
∴PE=

3

5

(10-2t)=-

6

5

t+6
即d=-

6

5

t+6…••（3分）

（2）∵S_△ABC=24，S_△PQC=

1

2

×PE×CQ=

1

2

×t×（-

6

5

t+6）=-

3

5

t²+3t…（4分）
∴S=S_△ABC-S_△PQC=

3

5

t2-3t+24，
即s=

3

5

t2-3t+24…（6分）

（3）假设四边形ABQP的面积是△CPQ面积的3倍，则有：

3

5

t2-3t+24=18，
即b²-4ac=-15＜0…（7分）
∵b²-4ac=-15＜0，方程无解，…（8分）
∴在P，Q两点移动的过程中，四边形ABQP的面积不可能是△CPQ面积的3倍…（9分）

点评：本题考查矩形的性质，同时涉及到了勾股定理、根的判别式、三角形的面积公式及平行线分线段成比例，是一道小的综合题，解题关键是对这些知识的熟练掌握及灵活运用．