题目内容
如图,已知AB是⊙O的直径,点C在⊙O上,P是△OAC的重心,且OP=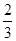 ,∠A=30º.
,∠A=30º.
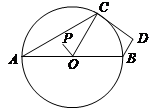
(1)求劣弧 的长;
的长;
(2)若∠ABD=120º,BD=1,求证:CD是⊙O的切线.
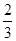 ,∠A=30º.
,∠A=30º.
(1)求劣弧
 的长;
的长;(2)若∠ABD=120º,BD=1,求证:CD是⊙O的切线.
(1) (2)要证明切线,即证明其与圆的直径成直角,利用全等三角形,可以求出对应角相等,进而证明出直角.
(2)要证明切线,即证明其与圆的直径成直角,利用全等三角形,可以求出对应角相等,进而证明出直角.
 (2)要证明切线,即证明其与圆的直径成直角,利用全等三角形,可以求出对应角相等,进而证明出直角.
(2)要证明切线,即证明其与圆的直径成直角,利用全等三角形,可以求出对应角相等,进而证明出直角.试题分析:(1)延长OP交AC于E,
∵P是△OAC的重心,
 ,
,∴
 ,
, 且 E是AC的中点.,∵
 ,∴OE⊥AC.
,∴OE⊥AC.在Rt△OAE中,∵
 ,
, ,∴
,∴ ∴
∴ 
∴
 . ∴
. ∴
(2)证明:连结BC.
∵E、O分别是线段AC、AB的中点,
∴BC∥OE,且BC=2OE=2=OB=OC.
∴△OBC是等边三角形. ∴∠OBC=60°.
∵∠OBD=120°,∴∠CBD=60°=∠AOE.
∵ BD=1=OE,BC=OA,∴△OAE ≌△BCD.
∴∠BCD=30°. ∵∠OCB=60°, ∴∠OCD=90°.
∴CD是⊙O的切线.
点评:题目难度一般,利用重心,可以知道线段为
 分段,学生可以尝试多做此类题目,一般来讲证明切线的题万变不离其宗
分段,学生可以尝试多做此类题目,一般来讲证明切线的题万变不离其宗
练习册系列答案
相关题目
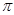 )
)


 .
.
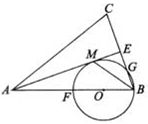
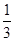 时,求⊙O的半径.
时,求⊙O的半径. 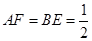 ,联结FC、ED,CD=2,AB=6。
,联结FC、ED,CD=2,AB=6。