题目内容
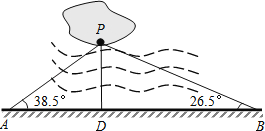
【题目】如图所示,PA、PB是⊙O的切线,A、B为切点,∠APB=80°,点C是⊙O上不同于A、B的任意一点,求∠ACB的度数.

【答案】①若C点在劣弧AB上,则∠ACB=130°;②若C点在优弧AB上,则∠ACB=50°.
【解析】
本题注意要分情况讨论:C点在劣弧AB上或点C点在优弧AB上.连接过切点的半径,根据四边形的内角和定理求得∠AOB的度数,进一步根据圆周角定理进行计算.
连接OA、OB,在AB弧上任取一点C,连接AC、BC.
∵PA、PB是⊙O的切线,A、B为切点,∴∠OAP=∠OBP=90°.
∵∠APB=80°,在四边形OAPB中,可得∠AOB=100°.
分两种情况讨论:
①若C点在劣弧AB上,则∠ACB=130°;
②若C点在优弧AB上,则∠ACB=50°.

练习册系列答案
相关题目
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如右表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是________环,乙的平均成绩是________环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
【题目】在弹性限度内,弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如下表,下列说法不正确的是( )
x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
y/cm | 20 | 20.5 | 21 | 21.5 | 22 | 22.5 |
A. x与y都是变量,且x是自变量,y是x的函数
B. 弹簧不挂重物时的长度为0 cm
C. 物体质量每增加1 kg,弹簧长度y增加0.5 cm
D. 所挂物体质量为7 kg时,弹簧长度为23.5 cm