题目内容
如图，在边长为1的正方形网格中，图①是边长为1的格点正方形，将图①正方形的各边顺次延长一倍后，连接其外端的4个格点便得到图②，我们称这样得到的图形为“拓展正方形”，按此规律可以得到一系列的“拓展正方形”．若图②是第1个拓展正方形，则第n个拓展正方形的面积为________．
5n-1
分析：先根据题中已知条件，求出每个正方形的边长，最后求面积．
解答：一个正方形的边长为1，即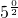
；由勾股定理得，第二个正方形边长为
=
，即
；由勾股定理得，第三个正方形边长为
=5，即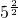
…第n个正方形的边长为
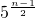，所以面积为5n-1．
点评：此题考查了图形的规律性，解答此题的关键是由所给正方形求出其边长与面积，找出规律．
分析：先根据题中已知条件，求出每个正方形的边长，最后求面积．
解答：一个正方形的边长为1，即
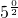；由勾股定理得，第二个正方形边长为=，即；由勾股定理得，第三个正方形边长为=5，即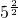…第n个正方形的边长为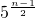，所以面积为5n-1．点评：此题考查了图形的规律性，解答此题的关键是由所给正方形求出其边长与面积，找出规律．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
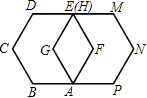如图，如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合，那么点B的对应点是点
已知：如图，在边长为a的正△ABC中，分别以A，B，C点为圆心，
如图，将边长为3的正六边形A1A2A3A4A5A6，在直线l上由图1的位置按顺时针方向向右作无滑动滚动，当A1第一次滚动到图2位置时，顶点A1所经过的路径的长为（ ）
已知：如图，在边长为a的正△ABC中，分别以A，B，C点为圆心，
长为半径作
，
，
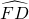，求阴影部分的面积．
长为半径作
，
，
，求阴影部分的面积．