题目内容
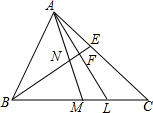 如图,AM、BE是△ABC的角平分线,AM交BE于N,AL⊥BE于F交BC于L,若∠ABC=2∠C,下列结论:①BE=EC;②BF=AE+EF;③AC=BM+BL;④∠MAL=
如图,AM、BE是△ABC的角平分线,AM交BE于N,AL⊥BE于F交BC于L,若∠ABC=2∠C,下列结论:①BE=EC;②BF=AE+EF;③AC=BM+BL;④∠MAL= ∠ABC,其中正确的结论是
∠ABC,其中正确的结论是
- A.①②③
- B.①④
- C.①②③④
- D.①②
C
分析:根据角平分线定义求出∠ABE=∠EBC=∠C,根据等角对等边求出BE=CE,即可判断①;
证△ABE∽△ACB,推出AB2=AE×AC,求出AF2=AB2-BF2=AE2-EF2,把 AB2=AE×AC代入入上式即可求出BF=AE+EF,即可判断②;
延长AB到N,使BN=BM,连接MN,证△AMC≌△AMN,△AFB≌△BLF,推出AB=BL,即可判断③;
设∠LAC=x°,∠LAM=y°,则∠BAM=∠MAC=(x+y)°,证△AFB≌△BLF推出∠BAF=∠BLF,∠BAF=∠BAM+∠MAL=x°+y°+y°,∠BLA=∠C+∠LAC=∠C+x°,得出方程x°+y°+y°=∠C+x°,求出∠C=2y°,∠ABC=4y°,即可判断④.
解答: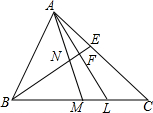 解:∵BE是∠ABC的角平分线,
解:∵BE是∠ABC的角平分线,
∴∠EBC=∠ABE= ∠ABC,
∠ABC,
∵∠ABC=2∠C,
∴∠ABE=∠EBC=∠C,
∴BE=EC,∴①正确;
∵∠ABE=∠ACB,∠BAC=∠EAB
∴△ABE∽△ACB,
∴ =
= ,
,
∴AB2=AE×AC,
在Rt△AFB与Rt△AFE中,由勾股定理得:AF2=AB2-BF2=AE2-EF2,
把 AB2=AE×AC代入入上式得:
AE×AC-BF2=AE2-EF2,
则BF2=AC×AE-AE2+EF2=AE×(AC-AE)+EF2=AE×EC+EF2=AE×BE+EF2,
即(BE-EF)2=AE×BE+EF2,
∴BE2-2BE×EF+EF2=AE×BE+EF2,
∴BE2-2BE×EF=AE×BE,
∴BE-2EF=AE,
BE-EF=AE+EF,
即BF=AE+EF,∴②正确;
延长AB到N,使BN=BM,连接MN,则△BMN为等腰三角形,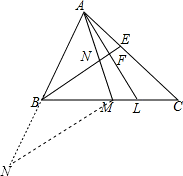
∴∠BNM=∠BMN,
△BNM的一个外角∠ABC=∠BNM+∠BMN=2∠BNM,
则∠BNM=∠ACB,
在△AMC与△AMN中
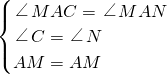 ,
,
∴△AMC≌△AMN(AAS),
∴AN=AC=AB+BN=AB+BM,
又∵AL⊥BE,
∴∠AFB=∠LFB=90°,
在△AFB与△LFB中,
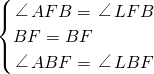 ,
,
∴△AFB≌△BLF(ASA),
∴AB=BL,
则AN=AC=AB+BN=AB+BM=BM+BL,即AC=BM+BL,∴③正确;
设∠LAC=x°,∠LAM=y°,
∵AM平分∠BAC,
∴∠BAM=∠MAC=(x+y)°.
∵△AFB≌△BLF,
∴∠BAF=∠BLF,
∵∠BAF=∠BAM+∠MAL=x°+y°+y°,∠BLA=∠C+∠LAC=∠C+x°,
∴x°+y°+y°=∠C+x°,
∴∠C=2y°,
∵∠ABC=2∠C,
∴∠ABC=4y°,
即∠MAL= ∠ABC,
∠ABC,
∴④正确.
故选C.
点评:本题考查了勾股定理,相似三角形的性质和判定,角平分线性质,相似三角形的性质和判定等知识点的综合运用.
分析:根据角平分线定义求出∠ABE=∠EBC=∠C,根据等角对等边求出BE=CE,即可判断①;
证△ABE∽△ACB,推出AB2=AE×AC,求出AF2=AB2-BF2=AE2-EF2,把 AB2=AE×AC代入入上式即可求出BF=AE+EF,即可判断②;
延长AB到N,使BN=BM,连接MN,证△AMC≌△AMN,△AFB≌△BLF,推出AB=BL,即可判断③;
设∠LAC=x°,∠LAM=y°,则∠BAM=∠MAC=(x+y)°,证△AFB≌△BLF推出∠BAF=∠BLF,∠BAF=∠BAM+∠MAL=x°+y°+y°,∠BLA=∠C+∠LAC=∠C+x°,得出方程x°+y°+y°=∠C+x°,求出∠C=2y°,∠ABC=4y°,即可判断④.
解答:
 解:∵BE是∠ABC的角平分线,
解:∵BE是∠ABC的角平分线,∴∠EBC=∠ABE=
 ∠ABC,
∠ABC,∵∠ABC=2∠C,
∴∠ABE=∠EBC=∠C,
∴BE=EC,∴①正确;
∵∠ABE=∠ACB,∠BAC=∠EAB
∴△ABE∽△ACB,
∴
 =
= ,
,∴AB2=AE×AC,
在Rt△AFB与Rt△AFE中,由勾股定理得:AF2=AB2-BF2=AE2-EF2,
把 AB2=AE×AC代入入上式得:
AE×AC-BF2=AE2-EF2,
则BF2=AC×AE-AE2+EF2=AE×(AC-AE)+EF2=AE×EC+EF2=AE×BE+EF2,
即(BE-EF)2=AE×BE+EF2,
∴BE2-2BE×EF+EF2=AE×BE+EF2,
∴BE2-2BE×EF=AE×BE,
∴BE-2EF=AE,
BE-EF=AE+EF,
即BF=AE+EF,∴②正确;
延长AB到N,使BN=BM,连接MN,则△BMN为等腰三角形,

∴∠BNM=∠BMN,
△BNM的一个外角∠ABC=∠BNM+∠BMN=2∠BNM,
则∠BNM=∠ACB,
在△AMC与△AMN中
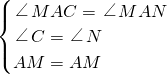 ,
,∴△AMC≌△AMN(AAS),
∴AN=AC=AB+BN=AB+BM,
又∵AL⊥BE,
∴∠AFB=∠LFB=90°,
在△AFB与△LFB中,
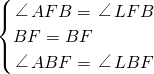 ,
,∴△AFB≌△BLF(ASA),
∴AB=BL,
则AN=AC=AB+BN=AB+BM=BM+BL,即AC=BM+BL,∴③正确;
设∠LAC=x°,∠LAM=y°,
∵AM平分∠BAC,
∴∠BAM=∠MAC=(x+y)°.
∵△AFB≌△BLF,
∴∠BAF=∠BLF,
∵∠BAF=∠BAM+∠MAL=x°+y°+y°,∠BLA=∠C+∠LAC=∠C+x°,
∴x°+y°+y°=∠C+x°,
∴∠C=2y°,
∵∠ABC=2∠C,
∴∠ABC=4y°,
即∠MAL=
 ∠ABC,
∠ABC,∴④正确.
故选C.
点评:本题考查了勾股定理,相似三角形的性质和判定,角平分线性质,相似三角形的性质和判定等知识点的综合运用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
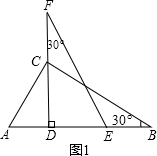


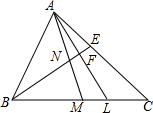 如图,AM、BE是△ABC的角平分线,AM交BE于N,AL⊥BE于F交BC于L,若∠ABC=2∠C,下列结论:①BE=EC;②BF=AE+EF;③AC=BM+BL;④∠MAL=
如图,AM、BE是△ABC的角平分线,AM交BE于N,AL⊥BE于F交BC于L,若∠ABC=2∠C,下列结论:①BE=EC;②BF=AE+EF;③AC=BM+BL;④∠MAL=