题目内容
 如图,一艘轮船由A港沿北偏东60°方向航行10km至B港,再沿北偏西30°方向航行10km到达C港.
如图,一艘轮船由A港沿北偏东60°方向航行10km至B港,再沿北偏西30°方向航行10km到达C港.(1)求A、C两港之间的距离(精确到1km)
(2)求点C相对于点A位置.
分析:(1)由题意得DAB+∠EBA=180°,由∠DAB=60°,∠CBE=30°,则∠ABC=90°,由勾股定理,从而得出AC的长;
(2)由∠FCA=∠DAC=60°-45°=15°,则C点在A点北偏东15°的方向上,距离A点10
km处的位置.
(2)由∠FCA=∠DAC=60°-45°=15°,则C点在A点北偏东15°的方向上,距离A点10
| 2 |
解答: 解:(1)∵DA∥EB,
解:(1)∵DA∥EB,
∴∠DAB+∠EBA=180°,
∵∠DAB=60°,∠CBE=30°,
∴∠ABC=90°,
∵AB=CB=10,
∴AC=
=10
≈14(km);
(2)∵∠FCA=∠DAC=60°-45°=15°,
∴C点在A点北偏东15°的方向上,
距离A点10
km处的位置.
 解:(1)∵DA∥EB,
解:(1)∵DA∥EB,∴∠DAB+∠EBA=180°,
∵∠DAB=60°,∠CBE=30°,
∴∠ABC=90°,
∵AB=CB=10,
∴AC=
| 102+102 |
| 2 |
(2)∵∠FCA=∠DAC=60°-45°=15°,
∴C点在A点北偏东15°的方向上,
距离A点10
| 2 |
点评:本题考查了解直角三角形的应用,方向角问题,是基础知识比较简单.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (1)求A、C两港之间的距离(精确到1km)
(1)求A、C两港之间的距离(精确到1km) 方向航行10km至B港,再沿北偏西
方向航行10km至B港,再沿北偏西 方向航行10km到达C港.
方向航行10km到达C港. (1)求A、C两港之间的距离(精确到1km)
(1)求A、C两港之间的距离(精确到1km) 方向航行10km至B港,再沿北偏西
方向航行10km至B港,再沿北偏西 方向航行10km到达C港.
方向航行10km到达C港. (1)求A、C两港之间的距离(精确到1km)
(1)求A、C两港之间的距离(精确到1km)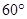 方向航行10km至B港,再沿北偏西
方向航行10km至B港,再沿北偏西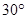 方向航行10km到达C港.
方向航行10km到达C港. (1)求A、C两港之间的距离(精确到1km)
(1)求A、C两港之间的距离(精确到1km)