题目内容
计算(每小题3分,共6分)
用适当的方法解下列方程(每小题4分,共8分)
(1)
(2)用配方法解方程:
(1) ,
, ;
;
(2) ,
, .
.
【解析】
试题分析:(1)先移项得到 ,然后利用因式分解法求解;
,然后利用因式分解法求解;
(2)先移项得到 ,根据完全平方公式把两边加上4得到
,根据完全平方公式把两边加上4得到 ,然后利用直接开平方法求解.
,然后利用直接开平方法求解.
试题解析:(1)移项得: ,分解因式得:
,分解因式得: ,
,
所以 ,所以
,所以 ,
, ;
;
(2) ,
, ,
, ,
, ,
,
所以 ,
, .
.
考点:1.解一元二次方程-因式分解法;2.解一元二次方程-配方法.
考点分析: 考点1:一元二次方程 定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:

它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中 ax2叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
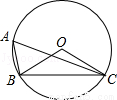
 中,
中, 为
为 的中点,连接
的中点,连接 并延长交
并延长交 的延长线于点
的延长线于点 .
.
 ;
; 与
与 满足什么数量关系时,四边形
满足什么数量关系时,四边形 是矩形,请说明理由.
是矩形,请说明理由.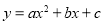 的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C (0,5),另抛物线经过点(1,8),M为它的顶点.
的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C (0,5),另抛物线经过点(1,8),M为它的顶点.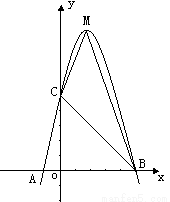
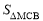 .
.
 向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )
向右平移1个单位,再向下平移2个单位,所得到的抛物线是( )



 = 。
= 。 的两个根是等腰三角形的底和腰,则这个等腰三角形周长为
的两个根是等腰三角形的底和腰,则这个等腰三角形周长为