题目内容
2.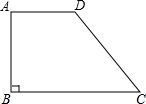 已知:在直角梯形ABCD中,AD∥BC,∠B=90°,∠ADC=135°,DC=8$\sqrt{2}$cm,以D为圆心,以8cm长为半径作⊙D.判断⊙D与BC有几个交点.
已知:在直角梯形ABCD中,AD∥BC,∠B=90°,∠ADC=135°,DC=8$\sqrt{2}$cm,以D为圆心,以8cm长为半径作⊙D.判断⊙D与BC有几个交点.
分析 过D作DE⊥BC于E,根据平行线的性质得到∠C=45°,推出DE=CE,于是求得DE=$\frac{\sqrt{2}}{2}$CD=8cm,即可得到结论.
解答  解:过D作DE⊥BC于E,
解:过D作DE⊥BC于E,
∵AD∥BC,∠ADC=135°,
∴∠C=45°,
∴∠CDE=45°,
∴DE=CE,
∵CD=8$\sqrt{2}$,
∴DE=$\frac{\sqrt{2}}{2}$CD=8cm,
∵⊙D半径为8cm,
∴⊙D与BC有1个交点.
点评 本题考查了直线与圆的位置关系,平行线的性质,等腰直角三角形的性质,勾股定理,正确的作出辅助线构造直角三角形是解题的关键.

练习册系列答案
相关题目
12.下列运算正确的是( )
| A. | -|-3|=3 | B. | -(-3)=3 | C. | 3ab-ab=3 | D. | -23=-6 |
17.已知抛物线的顶点坐标是P(1,3),且开口向下,下列说法正确的是( )
| A. | 当x≤1时,y随x的增大而减小 | B. | 当x≥1时,y随x的增大而增大 | ||
| C. | 当x<3时,y随x的增大而减小 | D. | 当x>3时,y随x的增大而减小 |
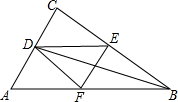 如图,Rt△ABC中,∠C=90°,角平分线BD交AC于D,DE∥AB交BC于E,点F为AB上一点,连结DF,EF.已知DC=5,CE=12,则△DEF的面积是( )
如图,Rt△ABC中,∠C=90°,角平分线BD交AC于D,DE∥AB交BC于E,点F为AB上一点,连结DF,EF.已知DC=5,CE=12,则△DEF的面积是( )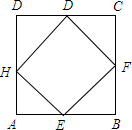 如图,长方形EFGH内接于边长为1的正方形ABCD,设AE=x,试求正方形EFGH的面积y与x的函数解析式,写出自变量x的取值范围,并求出AE=$\frac{1}{4}$时,正方形EFGH的面积.
如图,长方形EFGH内接于边长为1的正方形ABCD,设AE=x,试求正方形EFGH的面积y与x的函数解析式,写出自变量x的取值范围,并求出AE=$\frac{1}{4}$时,正方形EFGH的面积.