题目内容
8.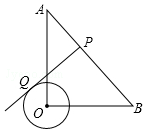 如图,在Rt△AOB中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB
如图,在Rt△AOB中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为$\sqrt{7}$.
分析 连接OP,OQ,由PQ为圆O的切线,利用切线的性质得到OQ与PQ垂直,利用勾股定理列出关系式,由OP最小时,PQ最短,根据垂线段最短得到OP垂直于AB时最短,利用面积法求出此时OP的值,再利用勾股定理即可求出PQ的最短值.
解答 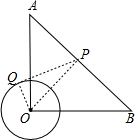 解:连接OP、OQ,如图所示,
解:连接OP、OQ,如图所示,
∵PQ是⊙O的切线,
∴OQ⊥PQ,
根据勾股定理知:PQ2=OP2-OQ2,
∴当PO⊥AB时,线段PQ最短,
∵在Rt△AOB中,OA=OB=4,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=4$\sqrt{2}$,
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$AB•OP,即OP=$\frac{OA•OB}{AB}$=2$\sqrt{2}$,
∴PQ=$\sqrt{O{P}^{2}-O{Q}^{2}}$=$\sqrt{(2\sqrt{2})^{2}-{1}^{2}}$=$\sqrt{7}$,
故答案为$\sqrt{7}$.
点评 此题考查了切线的性质,勾股定理的应用,熟练掌握切线的性质是解本题的关键,注意:圆的切线垂直于过切点的半径.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
13.已知函数y=$\frac{2x-1}{x+2}$,当x=3时,y的值为( )
| A. | 1 | B. | -1 | C. | -2 | D. | -3 |
18.为了鼓励农民发展生产,国家对购买农机的农户给予农机售价13%的政府补贴,某市农机公司一次性购进A,B两种型号的收割机共30台,根据市场需求,这些收割机可以全部销售.其中,收割机的进价和售价见下表:
设公司计划购进A型收割机x台.
(1)求收割机全部销售后公司获得的利润.(用含x的代数式表示)
(2)当x=10时,求收割机全部销售后公司获得的利润是多少.
| A型收割机 | B型收割机 | |
| 进价(万元/台) | 4 | 3 |
| 售价(万元/台) | 6 | 4 |
(1)求收割机全部销售后公司获得的利润.(用含x的代数式表示)
(2)当x=10时,求收割机全部销售后公司获得的利润是多少.

 某工厂要加工一批无底帐篷,设计者给出了帐篷的三视图,请你按照三视图确定制作每项帐篷所需布料的面积(图中尺寸单位:cm)
某工厂要加工一批无底帐篷,设计者给出了帐篷的三视图,请你按照三视图确定制作每项帐篷所需布料的面积(图中尺寸单位:cm)