题目内容
14.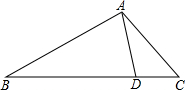 如图,D是△ABC的边BC上一点,已知AB=4,AD=2,∠DAC=∠B,若△ABD的面积为9,则△ACD的面积为3.
如图,D是△ABC的边BC上一点,已知AB=4,AD=2,∠DAC=∠B,若△ABD的面积为9,则△ACD的面积为3.
分析 首先证明△ACD∽△BCA,由相似三角形的性质可得:△ACD的面积:△ABC的面积为1:4,因为△ABD的面积为9,进而求出△ACD的面积.
解答 解:∵∠DAC=∠B,∠C=∠C,
∴△ACD∽△BCA,
∵AB=4,AD=2,
∴$\frac{{S}_{△ACD}}{{S}_{△ABC}}$=$\frac{{S}_{△ACD}}{{S}_{△ABD}{+S}_{△ACD}}$=$\frac{{S}_{△ACD}}{9+{S}_{△ACD}}$=$(\frac{1}{2})^{2}$=$\frac{1}{4}$
∴△ACD的面积=3,
故答案为:3.
点评 本题考查了相似三角形的判定和性质:相似三角形的面积比等于相似比的平方,是中考常见题型,解题关键是熟练掌握相似三角形的判定和性质.

练习册系列答案
相关题目
4.二次函数y=-(x+1)2-4的图象的顶点坐标是( )
| A. | (1,-4) | B. | (-1,4) | C. | (-1,-4) | D. | (1,4) |
5.已知实数a,b分别满足a2-6a+4=0,b2-6b+4=0,且a≠b,则a+b的值是( )
| A. | 4 | B. | -4 | C. | 6 | D. | -6 |
9.下列计算正确的是( )
| A. | ($\frac{1}{3}$)-2=9 | B. | $\sqrt{(-2)^{2}}$=-2 | C. | (-3)0=-1 | D. | |-7-5|=2 |
6.下列四个几何体中,左视图与其它三个不同的是( )
| A. |  | B. |  | C. |  | D. |  |
4.若分式方程$\frac{x}{x+2}=\frac{m}{x+2}$无解,则m的值为( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |