题目内容
9.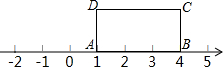 如图,在长方形ABCD中,边AB的长为3,AD的长为2,AB在数轴上,以原点A为圆心,AC的长为半径画弧,交负半轴于一点,则这个点表示的实数是1-$\sqrt{13}$.
如图,在长方形ABCD中,边AB的长为3,AD的长为2,AB在数轴上,以原点A为圆心,AC的长为半径画弧,交负半轴于一点,则这个点表示的实数是1-$\sqrt{13}$.
分析 连接AC,先根据勾股定理求出AC的长,再由数轴上两点间的距离公式即可得出结论.
解答  解:连接AC,
解:连接AC,
∵边AB的长为3,AD的长为2,
∴AC=$\sqrt{{AB}^{2}+{AD}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$.
∵A点为1,
∴这个点表示的实数是1-$\sqrt{13}$.
点评 本题考查的是实数与数轴,熟知实数与数轴上各点是一一对应关系是解答此题的关键.

练习册系列答案
相关题目
19.下列结论不正确的是( )
| A. | 若a>0,b<0,则a-b>0 | B. | 若a<0,b>0,则a-b<0 | ||
| C. | 若a<0,b<0,则a-(-b)>0 | D. | 若a<0,b<0,且|b|>|a|,则a-b>0 |
19.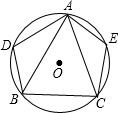 如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )
如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )
 如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )
如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )| A. | 220° | B. | 230° | C. | 240° | D. | 250°° |
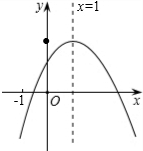 已知二次函数y=ax2+bx+c的图象如图所示,那么下列判断中
已知二次函数y=ax2+bx+c的图象如图所示,那么下列判断中 如图,在直角坐标系中,点A的坐标是(2,0),点B的坐标是(0,3),以AB为腰作等腰三角形,则另一顶点在坐标轴上的有4个.
如图,在直角坐标系中,点A的坐标是(2,0),点B的坐标是(0,3),以AB为腰作等腰三角形,则另一顶点在坐标轴上的有4个.