Question

如图，已知：A（m，2）是一次函数y=kx+b与反比例函数y=

3

x

的交点
（1）求m的值；
（2）若该一次函数分别与x轴y轴交于E、F两点，且直角△EOF的外心为点A．试求它的解析式；
（3）在y=

3

x

的图象上另取一点B，作BK⊥x轴于K，将（2）中的一次函数图象绕点A旋转后所得的直线记为l，若l与y轴的正半轴交于点C，且4CO=FO．试问：在y轴上是否存在点P，使得两个三角形的面积S_△PCA=S_△BOK？若存在，求点P的坐标，若不存在，请说明理由．

Answer 1

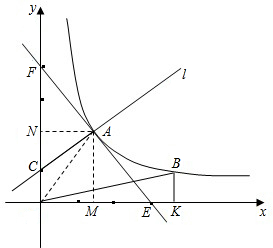
分析：（1）根据反比例函数的解析式求得m的值；
（2）根据直角三角形的外心是直角三角形的斜边的中点，由点A的坐标根据三角形的中位线定理可以求得点E，F的坐标，从而求得直线的解析式；
（3）根据反比例函数的解析式，得△BOK的面积是

3

2

．再根据点A的横坐标，知PC的长应是2．根据题意可以首先求得点C的坐标，再根据点P可能在点C的上方或下方进行分析．

解答：解：（1）把点A（m，2）代入反比例函数y=

3

x

中，得m=

3

2

（2分）

（2）根据直角三角形的外心是直角三角形的斜边的中点，则点A是EF的中点．又A（

3

2

，2），
∴E（3，0），F（0，4）
把E，F代入，得

3k+b=0 b=4

．解得

k=- 4 3 b=4

∴y=-

4

3

x+4（3分）

（3）原直线绕点A旋转所得直线交y轴的正半轴于C，且OC=

1

4

OF，F(0，4)
得C（0，1）
∵B（x_B，y_B）在y=

3

x

上，则有x_B•y_B=3，
由题意有S△BOK=

1

2

|xB•yB|=

3

2

（4分）
设y轴上点P（0，y_P），满足S_△PCA=S_△BOK
①若点P在点C上方，即y＞1，有S△PCA=

1

2

|yP-1|•|xA|=

1

2

(y-1)•

3

2

=

3

2

∴y=3，此时P（0，3）（3分）；
②若点P在点C下方，即y＜1，有S△PCA=

1

2

|yP-1|•|xA|=

1

2

(1-y)•

3

2

=

3

2

∴y=-1，此时P（0，-1）（2分）．

点评：能够根据函数的解析式求得点的坐标，能够根据点的坐标求得函数的解析式；掌握直角三角形的外心的位置；平行于x轴的线段的长等于两个点的横坐标的差的绝对值，平行于y轴的线段的长度等于两个点的纵坐标的差的绝对值．