题目内容
在⊙O中，AB是直径，F是圆周上异于A、B的一点，过F作切线l，若∠ABF=40°，则∠FAB=________度．
50
分析：根据直径所对的圆周角等于90°，再由三角形的内角和定理求得∠A．
解答：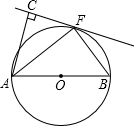
解：如图，
∵AB是直径，∴∠AFB=90°，
∵∠ABF=40°，∴∠FAB=50°，
故答案为50°．
点评：本题考查了切线的性质和圆周角定理，是基础知识比较简单．
分析：根据直径所对的圆周角等于90°，再由三角形的内角和定理求得∠A．
解答：
解：如图，∵AB是直径，∴∠AFB=90°，
∵∠ABF=40°，∴∠FAB=50°，
故答案为50°．
点评：本题考查了切线的性质和圆周角定理，是基础知识比较简单．
练习册系列答案
相关题目
4、如图，在⊙O中，AB是⊙O直径，∠BAC=40°，则∠ADC的度数是（ ）
（2013•海沧区一模）已知：在⊙O中，AB是直径，AC是弦，OE⊥AC于点E，过点C作直线FC，使∠FCA=∠AOE，交AB的延长线于点D．
（2012•邢台二模）如图，在⊙O中，AB是直径，∠OCA=26°，则∠BOC=（ ）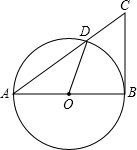
（2012•延庆县二模）已知：在⊙O中，AB是直径，CB是⊙O的切线，连接AC与⊙O交于点D，
（2012•宜宾）如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是