题目内容
 如图,BD为⊙O的直径,点A、C均在⊙O上,∠CBD=60°,则∠A的度数为
如图,BD为⊙O的直径,点A、C均在⊙O上,∠CBD=60°,则∠A的度数为
- A.60°
- B.30°
- C.45°
- D.20°
B
分析:首先根据直径所对的圆周角等于90°得到角BCD的度数,又根据题中已知的角CBD的度数,根据三角形的内角和定理得到角BDC的度数,然后根据同弧所对的圆周角相等,得到所求的角A与角BDC相等,即可得出正确的选项.
解答:在⊙O中,
∵BD是⊙O的直径,
∴∠BCD=90°,
又∵∠CBD=60°,
∴∠BDC=180°-∠BCD-∠CBD=30°,
根据同弧所对的圆周角相等,
则∠A=∠BDC=30°.
故选B.
点评:此题考查学生灵活运用直径所对的圆周角是直角,以及同弧所对圆周角相等等圆中的一些性质,考查了学生转化的数学思想,培养了学生的发散思维能力.
分析:首先根据直径所对的圆周角等于90°得到角BCD的度数,又根据题中已知的角CBD的度数,根据三角形的内角和定理得到角BDC的度数,然后根据同弧所对的圆周角相等,得到所求的角A与角BDC相等,即可得出正确的选项.
解答:在⊙O中,
∵BD是⊙O的直径,
∴∠BCD=90°,
又∵∠CBD=60°,
∴∠BDC=180°-∠BCD-∠CBD=30°,
根据同弧所对的圆周角相等,
则∠A=∠BDC=30°.
故选B.
点评:此题考查学生灵活运用直径所对的圆周角是直角,以及同弧所对圆周角相等等圆中的一些性质,考查了学生转化的数学思想,培养了学生的发散思维能力.

练习册系列答案
相关题目
 10、如图,一电线杆AB的影子分别落在了地上和墙上,某一时刻,小明竖起1米高的直杆,量得其影长为0.5米,此时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.小明用这些数据很快算出了电线杆AB的高.请你计算,电线杆AB的高为( )
10、如图,一电线杆AB的影子分别落在了地上和墙上,某一时刻,小明竖起1米高的直杆,量得其影长为0.5米,此时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.小明用这些数据很快算出了电线杆AB的高.请你计算,电线杆AB的高为( )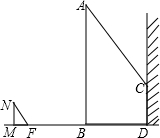 如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?
如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗? (2012•渝北区一模)如图,等边△ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让△ABC沿这条直线向右平移,直到点B与点E重合为止,设BD的长为x,△ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
(2012•渝北区一模)如图,等边△ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让△ABC沿这条直线向右平移,直到点B与点E重合为止,设BD的长为x,△ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
