题目内容
4.已知一个二次函数图象与x轴交于(-3,0),(1,0)两点,与y轴的交点为(0,4),求该二次函数的解析式.分析 由于已知抛物线与x轴的交点坐标,则可设交点式y=a(x+3)(x-1),然后把(0,4)代入求出a的值即可.
解答 解:设抛物线解析式为y=a(x+3)(x-1),
把(0,4)代入得a•3•(-1)=4,
解得a=-$\frac{4}{3}$,
所以抛物线解析式为y=-$\frac{4}{3}$(x+3)(x-1),即y=-$\frac{4}{3}$x2-$\frac{8}{3}$x+4.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
14.下列运算中结果正确的是( )
| A. | 3a+2b=5ab | B. | 3x2y-2x2y=x2y | C. | -3x+5x=-8x | D. | 5y-3y=2 |
15.下列图案中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.池塘中放养了鲤鱼2000条,鲢鱼若干,在几次随机捕捞中,共抓到鲤鱼400条,鲢鱼800条,估计池塘中原来放养了鲢鱼( )条.
| A. | 1000 | B. | 2000 | C. | 3000 | D. | 4000 |
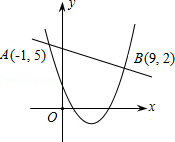 如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(-1,5)、B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为-1≤x≤9.
如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(-1,5)、B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为-1≤x≤9.