题目内容
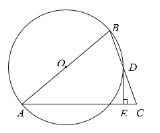
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,以线段
上,以线段![]() 的长为半径的
的长为半径的![]() 与
与![]() 相切于点
相切于点![]() ,
,![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() 并延长交
并延长交![]() 延长线于点
延长线于点![]() .
.
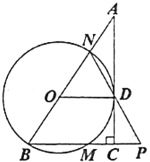
(1)求证:![]() ;
;
(2)已知![]() 的半径为5.
的半径为5.
①若![]() ,则
,则![]() __________;
__________;
②连接![]() ,当
,当![]() __________时,四边形
__________时,四边形![]() 是菱形.
是菱形.
【答案】(1)证明见解析;(2)①![]() ,②5.
,②5.
【解析】
(1)由AD是![]() 的切线推出
的切线推出![]() ,证得
,证得![]() ,推出∠OND
,推出∠OND![]() ,利用三角形的外角性质即可得出结论;
,利用三角形的外角性质即可得出结论;
(2)①由勾股定理求出AD的长,再利用ΔAOD∽ΔABC相似,即可求得CD的长;
②连接DM,OM,由菱形的性质得DM的长,进而求得MC,BC的长度,再利用ΔAOD∽ΔABC相似即可求得AN的长.
(1)证明:∵![]() 是
是![]() 的切线,∴
的切线,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
又∵![]() ,∴
,∴![]() .
.
∴![]() .
.
∴![]() .
.
(2)①在RtΔAOD中,OD=5,OA=ON+AN=8+5=13,
∴AD=![]() =
=![]() ,
,
∵![]() ,
,
∴ΔAOD∽ΔABC,
∴![]() 即
即![]() ,
,
∴CD=![]() ;
;
②如图,连接OM,DM

当四边形OBMD为菱形时,DM=BM=OB=OD=5
∵OM=5
∴ΔOMD是等边三角形,
∴∠ODM=60,
∴∠CDM=90-∠ODM=30,
在RtΔMCD中,MC=![]() DM=
DM=![]() ,
,
∴BC=BM+MC=5+![]() =
=![]() ,
,
由①ΔAOD∽ΔABC得![]() ,
,
即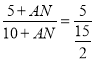 ,
,
∴AN=5,
当AN=5时,当四边形OBMD为菱形.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目