Question

【题目】如图，四边形中，，将绕点顺时针旋转一定角度后，点的对应点恰好与点重合，得到.

(1)请求出旋转角的度数；

(2)请判断与的位置关系，并说明理由；

(3)若，，试求出四边形的对角线的长.

Answer 1

【答案】(1)旋转角的度数为 ； (2)，理由见解析；(3).

【解析】

(1)根据旋转的性质可得：AC=BC,从而得到，再由三角形内角和得到∠ACB＝，即为旋转的角度;

(2)由旋转的性质可得，从而得到，由对顶角相等得，从而得到，即可得出结论;

(3) 连接,先证明△CDE是等腰直角三角形，再在Rt△ADE中，求出AE即可解决问题．

(1)∵将绕点顺时针旋转得到

∴

∴，

又∵，

∴，

∴

故旋转角的度数为

(2).理由如下：

在中，

∴

∵

∴

即

又∵

∴

∴

∴.

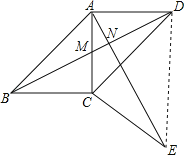
(3)如图，连接，

由旋转图形的性质可知

，旋转角

∴

∵，

∴

在中，

∴，

∵

∴

在中，

∴

∴