题目内容
把一个六个面分别标有数字1，2，3，4，5，6有正方体骰子随意掷一次，各个数字所在面朝上的机会均相等．
（1）若抛掷一次，则朝上的数字大于4的概率是多少？
（2）若连续抛掷两次，第一次所得的数为m，第二次所得的数为n．把m、n作为点A的横、纵坐标，那么点A（m、n）在函数y=3x-1的图象上的概率又是多少？
解：（1）依题意可知：随意掷一次正方体骰子，面朝上的数可能出现的结果有1、2、3、4、5、6共6种，而且它们出现的可能性相等．满足数字大于4（记为事件A）的有2种．所以P（A）=
（2）依题意列表分析如下：
由表可以看出，可能出现的结果有36种，而且它们出现的可能性相等．所得点A（记为事件A）的有（1 2）和（2 5）两种情况，所以在函数y=3x-1的图象上的概率为
P（A）=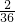
=
．
分析：（1）让大于4的数的个数除以数的总数即为所求的概率；
（2）列举出所有情况，看点A（m、n）在函数y=3x-1的图象上的情况数占总情况数的多少即可．
点评：考查概率的求法；用到的知识点为：概率=所求情况数与总情况数之比．得到所求的情况数是解决本题的易错点．
（2）依题意列表分析如下：
| 第二次n | |||||||
| 第 一 次 m | 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | （1 1） | （1 2） | （1 3） | （1 4） | （1 5） | （1 6） | |
| 2 | （2 1） | （2 2） | （2 3） | （2 4） | （2 5） | （2 6） | |
| 3 | （3 1） | （3 2） | （3 3） | （3 4） | （3 5） | （3 6） | |
| 4 | （4 1） | （4 2） | （4 3） | （4 4） | （4 5） | （4 6） | |
| 5 | （5 1） | （5 2） | （5 3） | （5 4） | （5 5） | （5 6） | |
| 6 | （6 1） | （6 2） | （6 3） | （6 4） | （6 5） | （6 6） | |
P（A）=
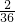=．分析：（1）让大于4的数的个数除以数的总数即为所求的概率；
（2）列举出所有情况，看点A（m、n）在函数y=3x-1的图象上的情况数占总情况数的多少即可．
点评：考查概率的求法；用到的知识点为：概率=所求情况数与总情况数之比．得到所求的情况数是解决本题的易错点．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目