题目内容
周长为6，面积为整数的直角三角形是否存在？若不存在，请给出证明；若存在，请证明共有几个？分析：设存在如上的直角三角形，设两直角边分别为a，b，斜边为c，根据题意可得出关于a、b、c的方程，由勾股定理可判断出c的取值范围，进而求出c的值，把c的值代入不定方程即可求出b、c的值，找出符合条件的未知数的对应值即可．
解答：解：设存在如上的直角三角形，设两直角边分别为a，b，斜边为c，
∵a+b+c=6（1）；
a2+b2=c2（2）
∴（a+b）2=（6-c）2（3）
∵
ab=9-3c为整数，
∴c为整数或以3为分母的分数；
∵直角三角形斜边最长则有c＞2，根据三角形三边边长规律有c＜3；
∴2＜c＜3；
∴c应为以3为分母的分数，c=
或
；
当c=
时，根据（1）（2）式有：b=6或
，a=-
或
，不合题意．
当c=
时，根据（1）（2）式有：b=
，a=
或a=
，b=
，
∴这样的直角三角形存在，恰有一个，两条直角边为
与
，斜边为
．
∵a+b+c=6（1）；
a2+b2=c2（2）
∴（a+b）2=（6-c）2（3）
∵
| 1 |
| 2 |
∴c为整数或以3为分母的分数；
∵直角三角形斜边最长则有c＞2，根据三角形三边边长规律有c＜3；
∴2＜c＜3；
∴c应为以3为分母的分数，c=
| 7 |
| 3 |
| 8 |
| 3 |
当c=
| 7 |
| 3 |
| 4 |
| 3 |
| 7 |
| 3 |
| 7 |
| 3 |
当c=
| 8 |
| 3 |
5-
| ||
| 3 |
5+
| ||
| 3 |
5-
| ||
| 3 |
5+
| ||
| 3 |
∴这样的直角三角形存在，恰有一个，两条直角边为
5-
| ||
| 3 |
5+
| ||
| 3 |
| 8 |
| 3 |
点评：本题考查的是非一次不定方程及勾股定理，根据题意判断出c的值是解答此题的关键．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
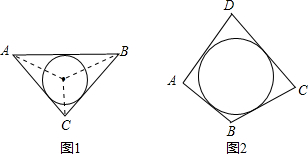阅读材料：如图1，△ABC的周长为l，面积为S，内切圆O的半径为r，探究r与S、l之间的关系．连接OA，OB，OC∵S=S△OAB+S△OBC+S△OCA