题目内容
已知如图,AB∥CD∥EF,点M、N、P分别在AB、CD、EF上,NQ平分∠MNP.

(1)若∠AMN=50º,∠EPN=70º,分别求∠MNP,∠DNQ的度数;
(2)若∠AMN= 度,∠EPN=
度,∠EPN= 度,请直接写出∠DNQ的度数(用含
度,请直接写出∠DNQ的度数(用含 ,
, 的代数式表示);
的代数式表示);
(3)试探究:∠DNQ与∠AMN,∠EPN之间的数量关系,并说明理由.
【答案】
(1)∠DNQ=10°;(2)∠DNQ= 度;(3)
度;(3)
【解析】
试题分析:(1)依题意知,∵AB∥CD∥EF,
∴∠MND=∠AMN=50°,∠DNP=∠EPN=70°,
∴∠MNP=∠MND+∠DNP=50°+70°=120°,
而NQ平分∠MNP,
∴∠MNQ= ∠MNP=
∠MNP= ×120°=60°,
×120°=60°,
∴∠DNQ=∠MNQ-∠MND=70°-60°=10°,
所以∠MNP、∠DNQ的度数分别为140°,10°
(2)由(1)可得∠DNQ = 度
度
(3)由(1)得∠MNP=∠MND+∠DNP=∠AMN+∠EPN,
∴∠MNQ= ∠MNP=
∠MNP= (∠AMN+∠EPN),
(∠AMN+∠EPN),
∴∠DNQ=∠MNQ-∠MND= (∠AMN+∠EPN)-∠AMN,
(∠AMN+∠EPN)-∠AMN,
∠DNQ= (∠END-∠AMN)..
(∠END-∠AMN)..
考点:平行线的性质
点评:本题难度中等,主要考查了平行线的性质:两直线平行,内错角相等.也考查了角平分线的定义.

练习册系列答案
相关题目
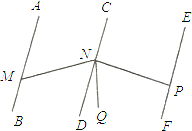 已知如图,AB∥CD∥EF,点M、N、P分别在AB、CD、EF上,NQ平分∠MNP.
已知如图,AB∥CD∥EF,点M、N、P分别在AB、CD、EF上,NQ平分∠MNP.
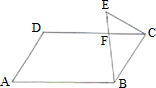 23、已知如图,AB∥CD,∠ABE=3∠DCE,∠DCE=28°,求E的度数.
23、已知如图,AB∥CD,∠ABE=3∠DCE,∠DCE=28°,求E的度数. 3、已知如图,AB∥CD,CN交AB于点M,若∠C=38°,则∠AMN=( )°.
3、已知如图,AB∥CD,CN交AB于点M,若∠C=38°,则∠AMN=( )°.