题目内容
如果点A(-3,y1),B(-2,y2),C(1,y3)都在反比例函数y=
(k>0)的图象上,那么,y1,y2,y3的大小关系是( )
| k |
| x |
| A、y1<y3<y2 |
| B、y2<y1<y3 |
| C、y1<y2<y3 |
| D、y3<y2<y1 |
考点:反比例函数图象上点的坐标特征
专题:计算题
分析:根据反比例函数图象上点的坐标特征,得到3y1=k,-2y2=k,1•y3=k,则可分别计算出y1,y2,y3的值,然后比较大小即可.
解答:解:∵A(-3,y1),B(-2,y2),C(1,y3)都在反比例函数y=
(k>0)的图象上,
∴-3y1=k,-2y2=k,1•y3=k,
∴y1=-
k,y2=-
k,y3=k,
而k>0,
∴y2<y1<y3.
故选B.
| k |
| x |
∴-3y1=k,-2y2=k,1•y3=k,
∴y1=-
| 1 |
| 3 |
| 1 |
| 2 |
而k>0,
∴y2<y1<y3.
故选B.
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=
(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
| k |
| x |

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 如图的几何体是由五个同样大小的正方体搭成的,其主视图是( )
如图的几何体是由五个同样大小的正方体搭成的,其主视图是( )A、 |
B、 |
C、 |
D、 |
方程3x-6=9的解是( )
| A、5 | ||
| B、1 | ||
C、
| ||
| D、-2 |
 如图,已知:∠A+∠B+∠C+∠D=360°,∠A=∠C,∠B=∠D.试说明:(1)AD∥BC,(2)AB∥CD.
如图,已知:∠A+∠B+∠C+∠D=360°,∠A=∠C,∠B=∠D.试说明:(1)AD∥BC,(2)AB∥CD.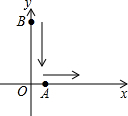 如图,两条直线互相垂直于点O,点A位于O处,以2cm/s的速度向右匀速移动,点B位于O的正上方18cm处,以3cm/s的速度与A同时开始向下匀速移动,多长时间时△AOB的面积为24cm2?
如图,两条直线互相垂直于点O,点A位于O处,以2cm/s的速度向右匀速移动,点B位于O的正上方18cm处,以3cm/s的速度与A同时开始向下匀速移动,多长时间时△AOB的面积为24cm2?