题目内容
第一象限内的点A在一反比例函数的图象上,过A作AB⊥x轴,垂足为B,连AO,已知△AOB的面积为4.

求反比例函数的解析式;
若点A的纵坐标为4,过点A的直线与x轴交于P,且△APB与△AOB相似,求所有符合条件的点P的坐标;
(3)在(2)的条件下,过点P、O、A的抛物线是否可由抛物线![]() 平移得到?若是,请说明由抛物线
平移得到?若是,请说明由抛物线![]() 如何平移得到;若不是,请说明理由.
如何平移得到;若不是,请说明理由.
答案:
解析:
解析:
|
解:(1)设反比例函数的解析式为 ∵S△AOB=4∴ (2)由题意得A(2,4)∴B(2,0) ∵点P在x轴上,设P点坐标为( ∴△ABP与△ABO相似有两种情况: 1°当△ABP∽△ABO时有 2°当△PBA∽△ABO时有 ∴P(10,0)或P(-6,0) ∴符合条件的点P坐标是(4,0)或(10,0)或(-6,0) (3)当点P坐标是(4,0)或(10,0)时,抛物线的开口向下 ∴不能由 当点P坐标是(-6,0)时,设抛物线解析式为 ∵抛物线过点A(2,4)∴ ∴该抛物线可以由 |

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 如图:第一象限内的点A在一反比例函数图象上,过点A作AB⊥x轴,垂足为B点,连接AO,已知△AOB的面积为4.①求反比例函数的解析式;②若点A的纵坐标为4,过点A的直线与x轴相交于点P,且△APB与△AOB相似,求所有符合条件的点P的坐标;③在②的条件下,求过P、O、A的抛物线的顶点坐标.
如图:第一象限内的点A在一反比例函数图象上,过点A作AB⊥x轴,垂足为B点,连接AO,已知△AOB的面积为4.①求反比例函数的解析式;②若点A的纵坐标为4,过点A的直线与x轴相交于点P,且△APB与△AOB相似,求所有符合条件的点P的坐标;③在②的条件下,求过P、O、A的抛物线的顶点坐标.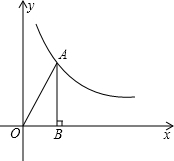 已知△AOB的面积为4.
已知△AOB的面积为4. 如图:第一象限内的点A在一反比例函数图象上,过点A作AB⊥x轴,垂足为B点,连接AO,已知△AOB的面积为4.①求反比例函数的解析式;②若点A的纵坐标为4,过点A的直线与x轴相交于点P,且△APB与△AOB相似,求所有符合条件的点P的坐标;③在②的条件下,求过P、O、A的抛物线的顶点坐标.
如图:第一象限内的点A在一反比例函数图象上,过点A作AB⊥x轴,垂足为B点,连接AO,已知△AOB的面积为4.①求反比例函数的解析式;②若点A的纵坐标为4,过点A的直线与x轴相交于点P,且△APB与△AOB相似,求所有符合条件的点P的坐标;③在②的条件下,求过P、O、A的抛物线的顶点坐标. 经过平移得到?若能,请说明由抛物线
经过平移得到?若能,请说明由抛物线 如何平移得到;若不能,请说明理由.
如何平移得到;若不能,请说明理由.
 经过平移得到?若能,请说明由抛物线
经过平移得到?若能,请说明由抛物线 如何平移得到;若不能,请说明理由.
如何平移得到;若不能,请说明理由.