题目内容

将一直线为10cm的圆形纸片剪成如图所示形状的纸片，再将纸片沿虚线折叠得到正方体形状的纸盒，则这样的纸盒体积最大为


  1. A.
    4cm3
  2. B.
    6cm3
  3. C.
    8cm3
  4. D.
    24cm3
C
分析：根据垂径定理和勾股定理求得正要想使正方体的体积最大，那么第2个图的两端2个正方形的顶点就应该都在圆上，设正方形的边长为x，根据勾股定理求出x即可．
解答：解：根据勾股定理求得正要想使正方体的体积最大，那么第2个图的两端2个正方形的顶点就应该都在圆上，设正方形的边长为x，
连接AB，则AB是直径，
AB=10，
在Rt△ABC中，由勾股定理得：AB2=AC2+BC2，
102=（3x）2+（4x）2，
解得：x=2，
因此正方体的体积就是2×2×2=8（cm3）．
故选：C．
点评：本题主要考查了正方形的性质及垂径定理等知识点，本题中根据垂径定理求出小正方形的边长是解题的关键．
练习册系列答案
相关题目
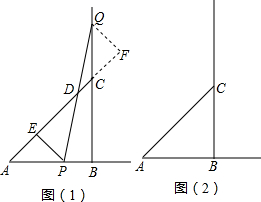（1）等腰△ABC的直角边AB=BC=10cm，点P、Q分别从A、C两点同时出发，均以1cm/秒的相同速度作直线运动，已知P沿射线AB运动，Q沿边BC的延长线运动，PQ与直线AC相交于点D，过P作PE⊥AC于点E．设P点运动时间为t．
①当点P在线段AB上运动时，线段DE的长度是否改变？若不改变，求出DE的值；若改变，请说明理由．
下面给出一种解题的思路，你可以按这一思路解题，也可以选择另外的方法解题．
解：过Q作QF⊥直线AC于点M
∵PE⊥AC于点E，QF⊥直线AC于点M
∴∠AEP=∠F=90°
（下面请你完成余下的解题过程）
②当点P在线段AB的延长线上运动时，（1）中的结论是否还成立？请在图2画出图形并说明理由．
（2）若将（1）中的“腰长为10cm的等腰直角△ABC”改为“边长为a的等边△ABC”时（其余条件不变），则线段DE的长度又如何？（直接写出答案，不需要解题过程）
（3）若将（2）中的“等边△ABC”改为“△ABC”（其余条件不变），请你做出猜想：当△ABC满足
∠A=∠ACB
∠A=∠ACB
条件时，（2）中的结论仍然成立．（直接写出答案，不需要解题过程）
将一直线为10cm的圆形纸片剪成如图所示形状的纸片，再将纸片沿虚线折叠得到正方体形状的纸盒，则这样的纸盒体积最大为（　　）

（1）等腰△ABC的直角边AB=BC=10cm，点P、Q分别从A、C两点同时出发，均以1cm/秒的相同速度作直线运动，已知P沿射线AB运动，Q沿边BC的延长线运动，PQ与直线AC相交于点D，过P作PE⊥AC于点E．设P点运动时间为t．
①当点P在线段AB上运动时，线段DE的长度是否改变？若不改变，求出DE的值；若改变，请说明理由．
下面给出一种解题的思路，你可以按这一思路解题，也可以选择另外的方法解题．
解：过Q作QF⊥直线AC于点M
∵PE⊥AC于点E，QF⊥直线AC于点M
∴∠AEP=∠F=90°
（下面请你完成余下的解题过程）
②当点P在线段AB的延长线上运动时，（1）中的结论是否还成立？请在图2画出图形并说明理由．
（2）若将（1）中的“腰长为10cm的等腰直角△ABC”改为“边长为a的等边△ABC”时（其余条件不变），则线段DE的长度又如何？（直接写出答案，不需要解题过程）
（3）若将（2）中的“等边△ABC”改为“△ABC”（其余条件不变），请你做出猜想：当△ABC满足________条件时，（2）中的结论仍然成立．（直接写出答案，不需要解题过程）
（1）等腰△ABC的直角边AB=BC=10cm，点P、Q分别从A、C两点同时出发，均以1cm/秒的相同速度作直线运动，已知P沿射线AB运动，Q沿边BC的延长线运动，PQ与直线AC相交于点D，过P作PE⊥AC于点E．设P点运动时间为t．
①当点P在线段AB上运动时，线段DE的长度是否改变？若不改变，求出DE的值；若改变，请说明理由．
下面给出一种解题的思路，你可以按这一思路解题，也可以选择另外的方法解题．
解：过Q作QF⊥直线AC于点M
∵PE⊥AC于点E，QF⊥直线AC于点M
∴∠AEP=∠F=90°
（下面请你完成余下的解题过程）
②当点P在线段AB的延长线上运动时，（1）中的结论是否还成立？请在图2画出图形并说明理由．
（2）若将（1）中的“腰长为10cm的等腰直角△ABC”改为“边长为a的等边△ABC”时（其余条件不变），则线段DE的长度又如何？（直接写出答案，不需要解题过程）
（3）若将（2）中的“等边△ABC”改为“△ABC”（其余条件不变），请你做出猜想：当△ABC满足______条件时，（2）中的结论仍然成立．（直接写出答案，不需要解题过程）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网