题目内容
已知x=
，y=
，且19x2+123xy+19y2=1985．试求正整数n．
解：化简x与y得：x=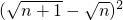
，y=
，
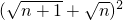∴x+y=4n+2，xy=1，
∴将xy=1代入方程，化简得：x2+y2=98，
∴（x+y）2=100，
∴x+y=10．
∴4n+2=10，
解得n=2．
分析：首先化简x与y，可得：x=（
）2=2n+1-2
，y=2n+1+2，所以x+y=4n+2，xy=1；将所得结果看作整体代入方程，化简即可求得．
点评：此题考查了二次根式的分母有理化．解题的关键是整体代入思想的应用．
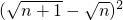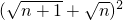，y=，∴x+y=4n+2，xy=1，
∴将xy=1代入方程，化简得：x2+y2=98，
∴（x+y）2=100，
∴x+y=10．
∴4n+2=10，
解得n=2．
分析：首先化简x与y，可得：x=（
）2=2n+1-2，y=2n+1+2，所以x+y=4n+2，xy=1；将所得结果看作整体代入方程，化简即可求得．点评：此题考查了二次根式的分母有理化．解题的关键是整体代入思想的应用．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
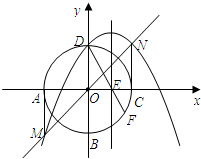C、D四点．过点A和点C分别作⊙O的切线MA、NC，它们分别与直线y=x交于点M、N，
已知直线l1∥l2，且 l3、l4和l1、l2分别交于A、B、C、D四点，点P在直线AB上运动．设∠ADP=∠1，∠DPC=∠2，∠BCP=∠3．