题目内容
已知ABCD是一个半径为R的圆的内接四边形,AB=12,CD=6,分别延长AB和DC,它们相交于P且BP=8,∠APD=60°,则R等于
- A.10
- B.2

- C.12

- D.14
B
分析:首先根据切割线定理即可计算出PC的长度是10,则PC= AP,以及,∠APD=60°,可以证明∠PCA=90°,在直角△ACD中根据勾股定理即可求得直径AD的长,从而求得半径的长.
AP,以及,∠APD=60°,可以证明∠PCA=90°,在直角△ACD中根据勾股定理即可求得直径AD的长,从而求得半径的长.
解答: 解:由切割线定理得PB•PA=PC•PD,
解:由切割线定理得PB•PA=PC•PD,
有 8×20=PC(PC+6).
解得PC=10.
如图,连接AC.
在△PAC中,由PA=2PC,∠APC=60°,得∠PCA=90°.
从而AD是圆的直径.由勾股定理,得
AD2=AC2+CD2=(PA2-PC2)+CD2=202-102+62=336.
∴AD= =4
=4
∴R= AD=2
AD=2 .
.
故选B.
点评:本题主要考查了切割线定理,正确判定△ACD是直角三角形是解题的关键.
分析:首先根据切割线定理即可计算出PC的长度是10,则PC=
 AP,以及,∠APD=60°,可以证明∠PCA=90°,在直角△ACD中根据勾股定理即可求得直径AD的长,从而求得半径的长.
AP,以及,∠APD=60°,可以证明∠PCA=90°,在直角△ACD中根据勾股定理即可求得直径AD的长,从而求得半径的长.解答:
 解:由切割线定理得PB•PA=PC•PD,
解:由切割线定理得PB•PA=PC•PD,有 8×20=PC(PC+6).
解得PC=10.
如图,连接AC.
在△PAC中,由PA=2PC,∠APC=60°,得∠PCA=90°.
从而AD是圆的直径.由勾股定理,得
AD2=AC2+CD2=(PA2-PC2)+CD2=202-102+62=336.
∴AD=
 =4
=4
∴R=
 AD=2
AD=2 .
.故选B.
点评:本题主要考查了切割线定理,正确判定△ACD是直角三角形是解题的关键.

练习册系列答案
相关题目
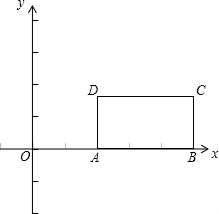 已知:矩形ABCD(字母顺序如图)的边长AB=3,AD=2,将此矩形放在平面直角坐标系xOy中,使AB在x轴正半轴上,而矩形的其它两个顶点在第一象限,且直线y=
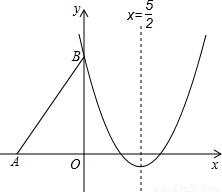
已知:矩形ABCD(字母顺序如图)的边长AB=3,AD=2,将此矩形放在平面直角坐标系xOy中,使AB在x轴正半轴上,而矩形的其它两个顶点在第一象限,且直线y=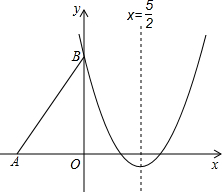 (2012•兰州)如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=
(2012•兰州)如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y= x2+bx+c经过点B,且顶点在直线x=
x2+bx+c经过点B,且顶点在直线x= 上.
上.
 x2+bx+c经过点B,且顶点在直线x=
x2+bx+c经过点B,且顶点在直线x= 上.
上.