题目内容
△ABC中，已知AB=AC=2.5cm，若∠B=30°，则BC边上的高等于________cm．
1.25
分析：先作出BC边上的高AD，在直角△ABD中，根据30°角所对的直角边等于斜边的一半即可求出AD的长．
解答：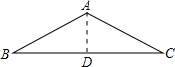
解：如图，作出BC边上的高AD，则AD⊥BC．
在直角△ABD中，∵∠ADB=90°，AB=2.5cm，∠B=30°，
∴AD=
AB=1.25cm．
即BC边上的高等于1.25cm．
故答案为1.25．
点评：此题主要考查直角三角形的性质，学会构造直角三角形，然后在直角三角形中利用30°角所对的直角边等于斜边的一半求解．
分析：先作出BC边上的高AD，在直角△ABD中，根据30°角所对的直角边等于斜边的一半即可求出AD的长．
解答：
解：如图，作出BC边上的高AD，则AD⊥BC．在直角△ABD中，∵∠ADB=90°，AB=2.5cm，∠B=30°，
∴AD=
AB=1.25cm．即BC边上的高等于1.25cm．
故答案为1.25．
点评：此题主要考查直角三角形的性质，学会构造直角三角形，然后在直角三角形中利用30°角所对的直角边等于斜边的一半求解．
练习册系列答案
相关题目
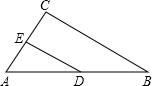如图，△ABC中，已知AB=8，BC=6，CA=4，DE是中位线，则DE=（ ）| A、4 | B、3 | C、2 | D、1 |
（2013•潮安县模拟）如图，△ABC中，已知AB=8，∠C=90°，∠A=30°，DE是中位线，则DE的长为（ ）