题目内容
已知点M、N的坐标分别为（0，1）、（0，－1），点P是抛物线
上的一个动点，过点N作平行于
轴的直线
。
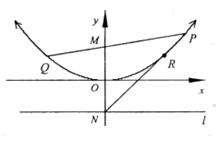
（1）求证：以点P为圆心，PM为半径的圆与直线相切；
（2）设直线PM，NP与抛物线的另一个交点分别为点Q，R，求证：Q，R两点关于
轴对称．
证明：（1）过点P作PA⊥
，垂足为A，过点M作MB⊥PA，垂足为B
∵P点在抛物线
上，
∴可设P点坐标为（
，
）
∵N（0，－1），∥
轴
∴A（，－1）
∴PA=
∴M（0，1）
∴B（，1）
∴PB=
∴
PA=PM
∴以点P为圆心，PM为半径的圆与直线相切
（2）设过点M的直线PQ的解析式为
，P点坐标为（，），Q点坐标为（
，
）
∴
，
∴
∴
∵
∴
设直线PN的解析式为
，
PN与抛物线的另一交点为R（
，
）
同理，可求得
∴
∵抛物线关于
轴对称
∴点Q与R关于轴对称.
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
里a＞0，且a为常数．直线EF和抛物线的对称轴交于点B，和直线x=2交于点D．
如图，已知点A、B的坐标分别是（0，0）（4，0），将△ABC绕A点按逆时针方向旋转90°后得到△A′B′C′
