题目内容
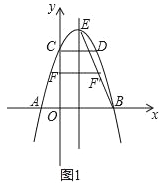
如图，二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点，与y轴交于点C，OB=OC，点D在函数图象上，CD∥x轴且CD=2，直线l是抛物线的对称轴，E是抛物线的顶点．
（1）求b、c的值；
（2）如图1，连BE，线段OC上的点F关于直线l的对称点F’恰好在线段BE上，求点F的坐标；
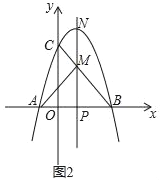
（3）如图2，动点P在线段OB上，过点P作x轴的垂线分别与BC交于点M、与抛物线交于点N．试问：抛物线上是否存在点Q，使得△PQN与△APM的面积相等，且线段NQ的长度最小？若存在，求出点Q的坐标；若不存在，说明理由．
练习册系列答案
相关题目
在学校开展的“争做最优秀中学生”的一次演讲比赛中，编号1，2，3，4，5的五位同学最
后成绩如下表所示：那么这五位同学演讲成绩的众数与中位数依次是 （ ）
参赛者编号 | 1 | 2 | 3 | 4 | 5 |
成绩/分 | 96 | 88 | 86 | 93 | 86 |
A. 96，88， B. 86，88, C. 88，86, D. 86，86
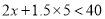B. 
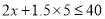
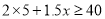D.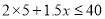 
=_____．
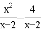