题目内容
 如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为4cm2,则该半圆的半径为( )
如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为4cm2,则该半圆的半径为( )分析:首先设圆心为A,大正方形的边长为2x,圆的半径为R,连接AC,AD,作AB⊥CM于点B,由勾股定理可得x2+4x2=(x+2)2+22,继而求得答案.
解答: 解:如图,圆心为A,设大正方形的边长为2x,圆的半径为R,连接AC,AD,作AB⊥CM于点B,
解:如图,圆心为A,设大正方形的边长为2x,圆的半径为R,连接AC,AD,作AB⊥CM于点B,
∴BC=CM,
∵正方形有两个顶点在半圆上,另外两个顶点在圆心两侧,
∴AE=BC=x,CE=2x;
∵小正方形的面积为4cm2,
∴小正方形的边长EF=DF=2,
由勾股定理得,R2=AE2+CE2=AF2+DF2,
即x2+4x2=(x+2)2+22,
解得,x=2,
∴R=2
cm.
故选C.
 解:如图,圆心为A,设大正方形的边长为2x,圆的半径为R,连接AC,AD,作AB⊥CM于点B,
解:如图,圆心为A,设大正方形的边长为2x,圆的半径为R,连接AC,AD,作AB⊥CM于点B,∴BC=CM,
∵正方形有两个顶点在半圆上,另外两个顶点在圆心两侧,
∴AE=BC=x,CE=2x;
∵小正方形的面积为4cm2,
∴小正方形的边长EF=DF=2,
由勾股定理得,R2=AE2+CE2=AF2+DF2,
即x2+4x2=(x+2)2+22,
解得,x=2,
∴R=2
| 5 |
故选C.
点评:此题考查了垂径定理、正方形的性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
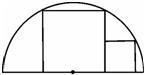 如图,两正方形彼此相邻且内接于半圆,若半圆的半径为5cm,则小正方形的边长为( )
如图,两正方形彼此相邻且内接于半圆,若半圆的半径为5cm,则小正方形的边长为( )| A、2cm | ||||
| B、2.5cm | ||||
C、
| ||||
D、
|
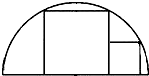 如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为1cm2,则该半圆的直径为
如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为1cm2,则该半圆的直径为 如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为( )
如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为( ) (2011•津南区一模)如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为
(2011•津南区一模)如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为