题目内容
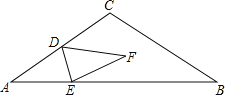
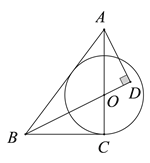
【题目】如图,在![]() 中,
中,![]() 为
为![]() 上一点,以
上一点,以![]() 为圆心,
为圆心,![]() 长为半径作圆,与
长为半径作圆,与![]() 相切于点
相切于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,且
,且![]() .
.
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]()
【解析】
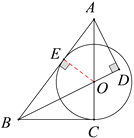
(1)作OE⊥AB于点E,证明△OBC≌△OBE,根据全等三角形的对应边相等可得OE=OC, OE是⊙O的半径 ,OE⊥AB ,即可判定AB为⊙O的切线;
(2)根据题意先求出AO、BO的长,再证明△AOD∽△BOC,根据相似三角形对应边成比例即可求出AD的长.
(1)作OE⊥AB于点E,
∵![]() 切BC于点C,
切BC于点C,
∴OC⊥BC,∠ACB=90°,
∵ AD⊥BD,∴∠D=90°,
∴∠ABD+∠BAD =90°,∠CBD+∠BOC=90°,
∵∠BOC=∠AOD,∠AOD=∠BAD,
∴∠BOC=∠BAD,
∴∠ABD=∠CBD
在△OBC和△OBE中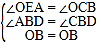 ,
,
∴△OBC≌△OBE,
∴OE=OC,∴OE是⊙O的半径 ,
∵OE⊥AB ,∴AB为⊙O的切线;
(2) ∵tan∠ABC=![]() ,BC=6,
,BC=6,
∴AC=8,∴AB=![]() ,
,
∵BE=BC=6,∴AE=4,
∵∠AOE=∠ABC,∴tan∠AOE=![]() ,∴EO=3,
,∴EO=3,
∴AO=5,OC=3,∴BO=![]() ,
,
在△AOD和△BOC中![]() ,
,
∴△AOD∽△BOC,∴![]() ,
,
即 ![]() ,∴AD=
,∴AD=![]() .
.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目