题目内容
如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心O.若∠B=20°,则∠C的大小等于( )
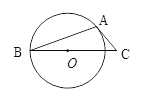
A. 20° B. 25° C. 40° D. 50°
练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
题目内容
如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心O.若∠B=20°,则∠C的大小等于( )

A. 20° B. 25° C. 40° D. 50°
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案