题目内容
已知: ,则
,则 =________.
=________.
8
分析:设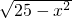 =a,
=a, =b,则a2+b2=40,把a-b=4两边平方可得到2ab=24,再利用完全平方公式(a+b)2=a2+2ab+b2即可计算出a+b的值.
=b,则a2+b2=40,把a-b=4两边平方可得到2ab=24,再利用完全平方公式(a+b)2=a2+2ab+b2即可计算出a+b的值.
解答:设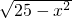 =a,
=a, =b,
=b,
∴a2+b2=40,
∵a-b=4,
∴(a-b)2=16,即a2-2ab+b2=16,
∴2ab=24,
∴(a+b)2=a2+2ab+b2=40+24=64,
∵a≥0,b≥0,
∴a+b=8.
故答案为8.
点评:本题考查了二次根式的化简求值:先根据已知条件把所求的代数式变形,然后利用整体的思想求值.
分析:设
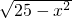 =a,
=a, =b,则a2+b2=40,把a-b=4两边平方可得到2ab=24,再利用完全平方公式(a+b)2=a2+2ab+b2即可计算出a+b的值.
=b,则a2+b2=40,把a-b=4两边平方可得到2ab=24,再利用完全平方公式(a+b)2=a2+2ab+b2即可计算出a+b的值.解答:设
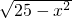 =a,
=a, =b,
=b,∴a2+b2=40,
∵a-b=4,
∴(a-b)2=16,即a2-2ab+b2=16,
∴2ab=24,
∴(a+b)2=a2+2ab+b2=40+24=64,
∵a≥0,b≥0,
∴a+b=8.
故答案为8.
点评:本题考查了二次根式的化简求值:先根据已知条件把所求的代数式变形,然后利用整体的思想求值.

练习册系列答案
相关题目
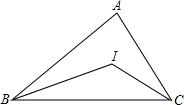 如图,△ABC中,∠ABC与∠ACB的平分线交于点I,根据下列条件,求∠BIC的度数.
如图,△ABC中,∠ABC与∠ACB的平分线交于点I,根据下列条件,求∠BIC的度数.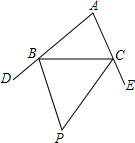
 6、如图,已知△ABC,则下列4个三角形中,与△ABC相似的是( )
6、如图,已知△ABC,则下列4个三角形中,与△ABC相似的是( ) 如图,在△ABC中,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,依此类推….已知∠A=α,则∠An的度数为
如图,在△ABC中,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,依此类推….已知∠A=α,则∠An的度数为