��Ŀ����
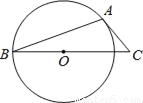
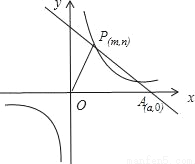
��֪��O������ԭ�㣬P��m��n����m��0���Ǻ���y=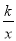 ��k��0���ϵĵ㣬����P��ֱ��PA��OP��P��ֱ��PA��x��������ύ�ڵ�A��a��0����a��m�������OPA�����Ϊs����s=1+
��k��0���ϵĵ㣬����P��ֱ��PA��OP��P��ֱ��PA��x��������ύ�ڵ�A��a��0����a��m�������OPA�����Ϊs����s=1+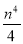 ��
��
��1����n=1ʱ�����A�����ꣻ
��2����OP=AP����k��ֵ��
��3����n��С��20����������k��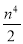 ����OP2����Сֵ��
����OP2����Сֵ��
��ϰ��ϵ�д�
 Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д� ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
�����Ŀ
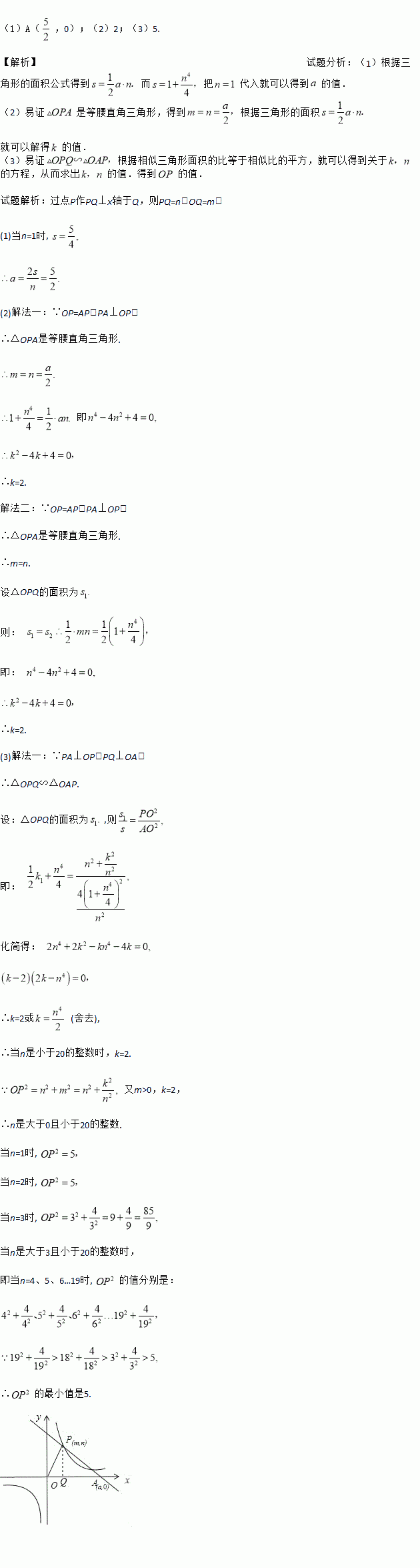

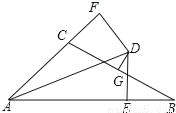
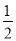 �ĵ����ǣ�������
�ĵ����ǣ�������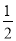 D. ��
D. ��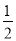
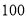 ����
����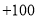 �ף���ô
�ף���ô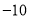 �ױ�ʾ��������__________��
�ױ�ʾ��������__________��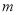 ��
��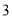 ����
����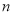 �IJ��ƽ��������ȷ���ǣ� ����
�IJ��ƽ��������ȷ���ǣ� ����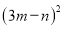 B.
B. 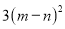 C.
C. 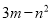 D.
D. 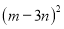
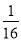 |������8��+[1������3��2]��
|������8��+[1������3��2]��