Question

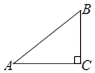
【题目】如图，在Rt△ABC中，∠ACB＝90°，AB＝6，cosB＝，先将△ACB绕着顶点C顺时针旋转90°，然后再将旋转后的三角形进行放大或缩小得到△A′CB′（点A′、C、B′的对应点分别是点A、C、B），连接A′A、B′B，如果△AA′B和△AA′B′相似，那么A′C的长是_____．

Answer 1

【答案】

【解析】

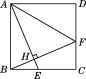
由题意当点A′在线段BC上且AA′平分∠BAC时，△AA′B和△AA′B′相似，作A′H⊥AB于H．证明△AA′H≌△AA′C（AAS），推出A′C＝A′H，AC＝AH＝2，设A′C＝A′H＝x，根据勾股定理构建方程即可解决问题．

由题意，当点A′在线段BC上且AA′平分∠BAC时，△AA′B和△AA′B′相似，作A′H⊥AB于H．

在Rt△ABC中，∵cosB＝，AB＝6，

∴BC＝4，AC＝＝2，

∵∠A′AH＝∠A′AC，∠AHA′＝∠ACA′＝90°，AA′＝AA′，

∴△AA′H≌△AA′C（AAS），

∴A′C＝A′H，AC＝AH＝2，设A′C＝A′H＝x，

在Rt△A′BH中，（4﹣x）2＝x2+（6﹣2）2，

∴x＝3﹣5，

∴A′C＝3﹣5，

故答案为：3﹣5．