题目内容
如图点P为弦AB上一点，连接OP，过P作PC⊥OP，PC交⊙O于点C，若AP=4，PB=2，则PC的长为
- A.
- B.2
- C.
- D.3
C
分析：首先延长CP交⊙O于点D，由PC⊥OP，根据垂径定理，即可得PC=PD，又由相交弦定理，即可得PC•PD=PB•PA，继而求得PC的长．
解答：
解：延长CP交⊙O于点D，
∵PC⊥OP，
∴PC=PD，
∵PC•PD=PB•PA，
∴PC2=PB•PA，
∵AP=4，PB=2，
∴PC2=8，
∴PC的长为：2．
故选C．
点评：此题考查了垂径定理与相交弦定理．此题难度不大，解题的关键是注意辅助线的作法与数形结合思想的应用．
分析：首先延长CP交⊙O于点D，由PC⊥OP，根据垂径定理，即可得PC=PD，又由相交弦定理，即可得PC•PD=PB•PA，继而求得PC的长．
解答：
解：延长CP交⊙O于点D，∵PC⊥OP，
∴PC=PD，
∵PC•PD=PB•PA，
∴PC2=PB•PA，
∵AP=4，PB=2，
∴PC2=8，
∴PC的长为：2
．故选C．
点评：此题考查了垂径定理与相交弦定理．此题难度不大，解题的关键是注意辅助线的作法与数形结合思想的应用．
练习册系列答案
相关题目
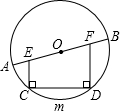E，DF⊥CD交AB于F，
；
，∴AB=
），C为直线AB上一点，过A、O、C的⊙E的半径为2．求线段OC的长．
，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB，AC于E，F，连结EF， 设⊙O半径为x， EF为y．①y关于x的函数关系式；②求线段EF长度的最小值．
；
感悟：圆内接三角形的一边和这边的对锐角、圆的半径(或直径)这三者关系，
），C为直线AB上一点，过A、O、C的⊙E的半径为2. 求线段OC的长。
，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB，AC于E，F，连结EF, 设⊙O半径为x, EF为y. 