题目内容
(2013•嘉定区一模)已知点A、B、C是半径长为2的半圆O上的三个点,其中点A是弧BC的中点(如图),联结AB、AC,点D、E分别在弦AB、AC上,且满足AD=CE.
(1)求证:OD=OE;
(2)联结BC,当BC=2
时,求∠DOE的度数;
(3)若∠BAC=120°,当点D在弦AB上运动时,四边形ADOE的面积是否变化?若变化,请简述理由;若不变化,请求出四边形ADOE的面积.

(1)求证:OD=OE;
(2)联结BC,当BC=2
| 2 |
(3)若∠BAC=120°,当点D在弦AB上运动时,四边形ADOE的面积是否变化?若变化,请简述理由;若不变化,请求出四边形ADOE的面积.

分析:(1)先证出△AOB≌△AOC,∠CAO=∠ABO,再根据BD=AE,证出△BOD≌△AOE,即可得出OD=OE;
(2)设OA和BC交于M,得出∠AOB=∠AOC,∠BOD=∠AOE,∠AOD=∠COE,则∠DOE=
∠BOC,∠AOC=
∠BOC,再根据AB=AC,得出OA⊥BC,CM=
BC=
,最后根据sin∠COM=
=
,得出∠COM=45°,∠BOC=90°,∠DOE=
∠BOC=45°;
(3)先证出S△AOB=S△AOC,S△BOD=S△AOE,S△AOB-S△BOD=S△AOC-S△AOE,S△AOD=S△COE,得出S△AOE+S△AOD=S△BOD+S△COE,S四边形ADOE=
S四边形ABOC,即可证出当点D在弦AB上运动时,四边形ADOE的面积没有变化,再根据∠ABC=120°,得出∠OAB=∠OAC=60°,ABOC是菱形,再求出AM=1,BC=2
,得出S菱形ABOC=2
,最后根据S四边形ADOE=
S四边形ABOC即可得出答案.
(2)设OA和BC交于M,得出∠AOB=∠AOC,∠BOD=∠AOE,∠AOD=∠COE,则∠DOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| CM |
| OC |
| ||
| 2 |
| 1 |
| 2 |
(3)先证出S△AOB=S△AOC,S△BOD=S△AOE,S△AOB-S△BOD=S△AOC-S△AOE,S△AOD=S△COE,得出S△AOE+S△AOD=S△BOD+S△COE,S四边形ADOE=
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
解答: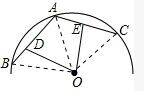 解:(1)∵A是弧BC的中点,
解:(1)∵A是弧BC的中点,
∴AB=AC,
连接OB、OA、OC,
∵在△AOB和△AOC中,
,
∴△AOB≌△AOC(SSS),
∴∠CAO=∠ABO,
∵AD=CE,
∴AB-AD=AC-CE,
即BD=AE,
∵在△BOD和△AOE中,
,
∴△BOD≌△AOE(SAS),
∴OD=OE;
(2)设OA和BC交于M,
∵△AOB≌△AOC,
∴∠AOB=∠AOC,
∵△BOD≌△AOE,
∴∠BOD=∠AOE,
∴∠AOD=∠COE,
∴∠DOE=∠AOE+∠AOD=
∠BOC,
∠AOC=∠AOE+∠COE=
∠BOC,
∵AB=AC,
∴OA⊥BC,CM=
BC=
,
∴sin∠COM=
=
,
∴∠COM=45°,
∴∠BOC=90°,
∴∠DOE=
∠BOC=45°;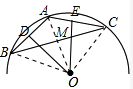
(3)∵△AOB≌△AOC,
∴S△AOB=S△AOC,
∵△BOD≌△AOE,
∴S△BOD=S△AOE,
∴S△AOB-S△BOD=S△AOC-S△AOE,
∴S△AOD=S△COE,
∴S△AOE+S△AOD=S△BOD+S△COE,
∴S四边形ADOE=
S四边形ABOC,
∴当点D在弦AB上运动时,四边形ADOE的面积没有变化,
∵∠BAC=120°,
∴∠OAB=∠OAC=60°,
∴ABOC是菱形,
∴AM=
AO=1
CM=
=
=
,
∴BC=2
,
∴S菱形ABOC=
×2
×2=2
,
∴S四边形ADOE=
S四边形ABOC=
.
 解:(1)∵A是弧BC的中点,
解:(1)∵A是弧BC的中点,∴AB=AC,
连接OB、OA、OC,
∵在△AOB和△AOC中,
|
∴△AOB≌△AOC(SSS),
∴∠CAO=∠ABO,
∵AD=CE,
∴AB-AD=AC-CE,
即BD=AE,
∵在△BOD和△AOE中,
|
∴△BOD≌△AOE(SAS),
∴OD=OE;
(2)设OA和BC交于M,
∵△AOB≌△AOC,
∴∠AOB=∠AOC,
∵△BOD≌△AOE,
∴∠BOD=∠AOE,
∴∠AOD=∠COE,
∴∠DOE=∠AOE+∠AOD=
| 1 |
| 2 |
∠AOC=∠AOE+∠COE=
| 1 |
| 2 |
∵AB=AC,
∴OA⊥BC,CM=
| 1 |
| 2 |
| 2 |
∴sin∠COM=
| CM |
| OC |
| ||
| 2 |
∴∠COM=45°,
∴∠BOC=90°,
∴∠DOE=
| 1 |
| 2 |

(3)∵△AOB≌△AOC,
∴S△AOB=S△AOC,
∵△BOD≌△AOE,
∴S△BOD=S△AOE,
∴S△AOB-S△BOD=S△AOC-S△AOE,
∴S△AOD=S△COE,
∴S△AOE+S△AOD=S△BOD+S△COE,
∴S四边形ADOE=
| 1 |
| 2 |
∴当点D在弦AB上运动时,四边形ADOE的面积没有变化,
∵∠BAC=120°,
∴∠OAB=∠OAC=60°,
∴ABOC是菱形,
∴AM=
| 1 |
| 2 |
CM=
| AC2-AM2 |
| 22-12 |
| 3 |
∴BC=2
| 3 |
∴S菱形ABOC=
| 1 |
| 2 |
| 3 |
| 3 |
∴S四边形ADOE=
| 1 |
| 2 |
| 3 |
点评:此题考查了圆的综合,用到的知识点是垂径定理、菱形的判定与性质、全等三角形的判定与性质、勾股定理等,关键是综合应用有关知识,列出算式.

练习册系列答案
相关题目
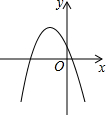 (2013•嘉定区一模)已知抛物线y=-x2+bx+c如图所示,那么b、c的取值范围是( )
(2013•嘉定区一模)已知抛物线y=-x2+bx+c如图所示,那么b、c的取值范围是( )