题目内容
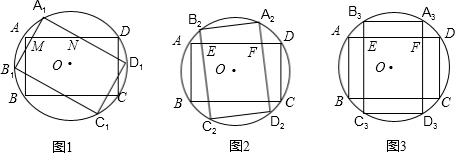
如图,矩形 A1B1C1D1的边长 A1D1=8,A1B1=6,顺次连接 A1B1C1D1各边的中点得到 A2B2C2D2,顺次连接A2B2C2D2各边的中点得到A3B3C3D3,…,依此类推.(1)求四边形A2B2C2D2的边长,并证明四边形A2B2C2D2是菱形;
(2)四边形A10B10C10D10是矩形还是菱形?A10B10=?(第(2)问写出结果即可)

分析:(1)由已知,先连接A1C1,B1D1,根据三角形中位线的性质,得A2B2=C2D2=
A1C1,A2D2=B2C2=
B1D1,又由矩形的性质对角线相等,推出四边形A2B2C2D2是菱形.由勾股定理求出对角线的长,从而求出四边形A2B2C2D2的边长.
(2)通过观察计算发现规律,An+2Bn+2Cn+2Dn+2与AnBnCnDn相似,且An+2Bn+2Cn+2Dn+2的边长是AnBnCnDn边长的一半,例如,A3B3C3D3的边长是A1B1C1D1边长的一半,A4B4C4D4的边长是A2B2C2D2边长的一半…,从而得出
A10B10C10D10也是菱形.
| 1 |
| 2 |
| 1 |
| 2 |
(2)通过观察计算发现规律,An+2Bn+2Cn+2Dn+2与AnBnCnDn相似,且An+2Bn+2Cn+2Dn+2的边长是AnBnCnDn边长的一半,例如,A3B3C3D3的边长是A1B1C1D1边长的一半,A4B4C4D4的边长是A2B2C2D2边长的一半…,从而得出
A10B10C10D10也是菱形.
解答: 解:连接A1C1,B1D1,
解:连接A1C1,B1D1,
已知A1B1C1D1是矩形,∴A1C1=B1D1,
又A2,B2,C2,D2是中点,根据三角形中位线性质得:
A2B2=C2D2=
A1C1,A2D2=B2C2=
B1D1,
∴A2B2=C2D2=A2D2=B2C2,
∴四边形A2B2C2D2是菱形.
在直角三角形A1B1C1中,根据勾股定理得:
A1C1=
=
=10,
∴A2B2=
A1C1=
×10=5.
所以四边形A2B2C2D2的边长为5.
(2)通过观察分析总结各个图形有如下关系:
An+2Bn+2Cn+2Dn+2与AnBnCnDn相似,且
An+2Bn+2Cn+2Dn+2的边长是AnBnCnDn边长的一半,
例如,A3B3C3D3的边长是A1B1C1D1边长的一半,A4B4C4D4的边长是A2B2C2D2边长的一半…
因此A10B10C10D10的边长是A2B2C2D2 的(
)5=
,
所以A10B10C10D10也是菱形. A10B10=
=
.
 解:连接A1C1,B1D1,
解:连接A1C1,B1D1,已知A1B1C1D1是矩形,∴A1C1=B1D1,
又A2,B2,C2,D2是中点,根据三角形中位线性质得:
A2B2=C2D2=
| 1 |
| 2 |
| 1 |
| 2 |
∴A2B2=C2D2=A2D2=B2C2,
∴四边形A2B2C2D2是菱形.
在直角三角形A1B1C1中,根据勾股定理得:
A1C1=
| A1B12+B1C12 |
| 62+82 |
∴A2B2=
| 1 |
| 2 |
| 1 |
| 2 |
所以四边形A2B2C2D2的边长为5.
(2)通过观察分析总结各个图形有如下关系:
An+2Bn+2Cn+2Dn+2与AnBnCnDn相似,且
An+2Bn+2Cn+2Dn+2的边长是AnBnCnDn边长的一半,
例如,A3B3C3D3的边长是A1B1C1D1边长的一半,A4B4C4D4的边长是A2B2C2D2边长的一半…
因此A10B10C10D10的边长是A2B2C2D2 的(
| 1 |
| 2 |
| 1 |
| 32 |
所以A10B10C10D10也是菱形. A10B10=
| A2B2 |
| 32 |
| 5 |
| 32 |
点评:此题考查的知识点是矩形的判定与性质、三角形中位线定理及菱形的判定,解答此题的关键是由已知和三角形中位线定理得出四边形A2B2C2D2是菱形,得出四边形A2B2C2D2的边长.通过观察计算找出规律推出A10B10C10D10也是菱形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目