题目内容
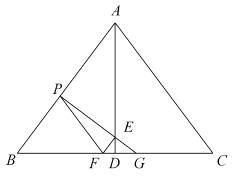
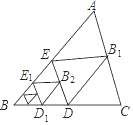
【题目】如图，将
沿着过
的中点
的直线折叠，使点
落在
边上的
处，称为第一次操作，折痕
到的距离为
；还原纸片后，再将
沿着过
的中点
的直线折叠，使点落在边上的
处，称为第二次操作，折痕
到的距离记为
；按上述方法不断操作下去……经过第
次操作后得到折痕
，到的距离记为
．若
，则的值为（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
根据中点的性质及折叠的性质可得DA=DA'=DB，从而可得∠ADA'=2∠B，结合折叠的性质可得∠ADA'=2∠ADE，可得∠ADE=∠B，继而判断DE∥BC，得出DE是△ABC的中位线，证得AA
⊥BC，得到AA=2，求出
=2-1，同理
，于是经过第n次操作后得到的折痕
∵
是
的中点，折痕
到
的距离为
∴点
到的距离
，
∵
是
的中点，折痕
到的距离记为
，
∴点到的距离
，
同理：
，
……
故选：C．
练习册系列答案
相关题目
【题目】某校为了解学生的课外阅读情况，随机调查了部分学生平均每天的课外阅读时间，并根据调查结果制成被调查学生人数的统计图表如下，但信息不完整．
时间(小时) | 0.5 | 1 | 1.5 | 2 |
人数 | 2 | 5 | 3 |
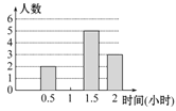
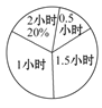
请根据所提供信息，解决下列问题：
（1）求扇形统计图中，读书时间为“2小时”部分的圆心角的度数．
（2）通过计算估计全校每个学生平均每天的课外阅读时间．
（3）从被调查的课外读书时间最少和最多的学生中，随机抽2个学生进行访谈，求各抽到1人的概率．
