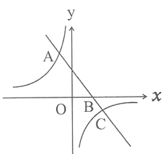
题目内容
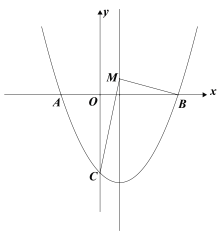
【题目】如图,直线![]() 与双曲线
与双曲线![]() 的图象相交于点A和点C,点A的坐标为
的图象相交于点A和点C,点A的坐标为![]() ,点C的坐标为
,点C的坐标为![]() .
.
(1)求![]() 的值和反比例函数的解析式;
的值和反比例函数的解析式;
(2)求![]() 的值,并写出在
的值,并写出在![]() 轴右侧,使得反比例函数大于一次函数的值的
轴右侧,使得反比例函数大于一次函数的值的![]() 的取值范围;
的取值范围;
(3)如图,直线![]() 与
与![]() 轴相交于点B,在
轴相交于点B,在![]() 轴上存在点D,使得
轴上存在点D,使得![]() 是以BC为腰的等腰三角形,求点D的坐标.
是以BC为腰的等腰三角形,求点D的坐标.
【答案】(1)4,![]() ;(2)4,
;(2)4,![]() ;(3)(3+
;(3)(3+![]() ,0)或(3-
,0)或(3-![]() ,0)或(5,0)
,0)或(5,0)
【解析】
(1)把![]() 代入
代入![]() 即可求出a,把
即可求出a,把![]() 代入
代入![]() 得反比例函数解析式;
得反比例函数解析式;
(2)把![]() 代入
代入![]() 即可求b,根据图象即可写出反比例函数大于一次函数的值的
即可求b,根据图象即可写出反比例函数大于一次函数的值的![]() 的取值范围;
的取值范围;
(3)求出点B坐标,根据勾股定理求出BC长,分当![]() 或BC=DC两类讨论即可求解.
或BC=DC两类讨论即可求解.
解:(1)把![]() 代入
代入![]() 得,
得,
![]() ,
,
∴![]() ,
,
把![]() 代入
代入![]() 得,
得,
![]() ,
,
![]() ,
,
∴![]() ;
;
(2)把![]() 代入
代入![]() 得
得![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 轴右侧,使得反比例函数大于一次函数的值的
轴右侧,使得反比例函数大于一次函数的值的![]() 的取值范围为:
的取值范围为:![]() ;
;
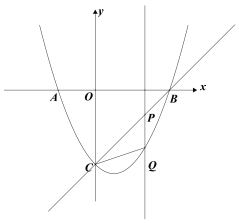
(3)如图:过点![]() 作
作![]() ⊥
⊥![]() 轴于点
轴于点![]() ,
,
把![]() 代入
代入![]() 得
得![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ,
,
当![]() 时,
时,![]() 或
或![]() ,
,
当BC=DC时,
∵CH⊥BD,
∴BH=HD=1,
∴OD=OH+HD=4+1=5,
∴D(5,0) ,
∴D(3+![]() ,0)或(3-
,0)或(3-![]() ,0)或(5,0).
,0)或(5,0).


练习册系列答案
相关题目