题目内容
已知：如图，四边形ABCD中，BC=CD=DB，∠ADB=90°，sin∠ABD=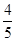
，S△BCD=
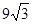. 求四边形ABCD的周长.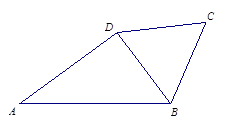
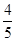，S△BCD=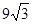. 求四边形ABCD的周长..解：过C作CE⊥BD于E.
∵∠ADB=90°，sin∠ABD=，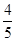
∴AD="4x,AB=5x." ………………………..1分
∴DB=3x
∵BC=CD=DB，
∴DE=
，∠CDB=60°. ………………………2分
∴tan∠CDB=
∴CE=
. ……………………………3分
∵S△BCD=,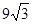
∴
∴ x=2. ………………………………………….4分
∴AD=8,AB=10,CD=CB=6.
∴四边形ABCD的周长="AD+AB+CD+CB=30." ……………………………..5分
∵∠ADB=90°，sin∠ABD=
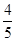，∴AD="4x,AB=5x." ………………………..1分
∴DB=3x
∵BC=CD=DB，
∴DE=
，∠CDB=60°. ………………………2分∴tan∠CDB=
∴CE=
. ……………………………3分∵S△BCD=
,∴
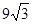∴ x=2. ………………………………………….4分
∴AD=8,AB=10,CD=CB=6.
∴四边形ABCD的周长="AD+AB+CD+CB=30." ……………………………..5分
过C作CE⊥BD，建立直角三角形，利用勾股定理和三角函数进行计算。
练习册系列答案
相关题目
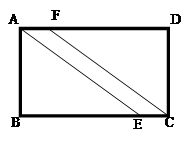
中，E、F、G、H分别是AB、BC、CD、DA上的点，且AE=CG，BF=DH．求证：
≌
．
以DE为折痕向右折叠，AE与BC交于点F，则
的面积为（ ）
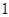，按图中所示的规律，用2012个这样的三角形镶嵌而成的四边形的周长是 .