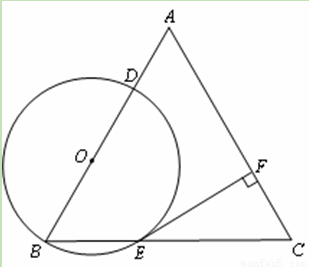
题目内容
已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
(1)证明见解析(2) 解析:
解析:
(1)证明:连接OE,则OB=OE.………………1分
∵△ABC是等边三角形, ∴∠ABC=∠C=60°.
∴△OBE是等边三角形.
∴∠OEB=∠C =60°. ∴OE∥AC.
∵EF⊥AC,∴∠EFC=90°.
∴∠OEF=∠EFC=90°.
∴EF是⊙O的切线.……………………4分
(2)连接DF,
∵DF是⊙O的切线, ∴∠ADF=90°.
设⊙O的半径为r,则BE=r,EC= ,AD=
,AD= .
.
在Rt△ADF中,∵∠A=60°, ∴AF=2AD= .
.
∴FC= .
.
在Rt△CEF中 ∵∠C=60°, ∴EC=2FC
∴ =2(
=2( ).
).
解得 .∴⊙O的半径是
.∴⊙O的半径是 .…………………………8分
.…………………………8分
注:其他解法对应给分。
(1)连接OE,利用等边三角形的性质求出OE∥AC,从而求得∠OEF=90°,得出结论
(2)连接DF,利用切线的性质直角三角形的性质求⊙O的半径
 解析:
解析:(1)证明:连接OE,则OB=OE.………………1分
∵△ABC是等边三角形, ∴∠ABC=∠C=60°.
∴△OBE是等边三角形.
∴∠OEB=∠C =60°. ∴OE∥AC.
∵EF⊥AC,∴∠EFC=90°.
∴∠OEF=∠EFC=90°.
∴EF是⊙O的切线.……………………4分
(2)连接DF,

∵DF是⊙O的切线, ∴∠ADF=90°.
设⊙O的半径为r,则BE=r,EC=
 ,AD=
,AD= .
.在Rt△ADF中,∵∠A=60°, ∴AF=2AD=
 .
.∴FC=
 .
.在Rt△CEF中 ∵∠C=60°, ∴EC=2FC
∴
 =2(
=2( ).
).解得
 .∴⊙O的半径是
.∴⊙O的半径是 .…………………………8分
.…………………………8分注:其他解法对应给分。
(1)连接OE,利用等边三角形的性质求出OE∥AC,从而求得∠OEF=90°,得出结论
(2)连接DF,利用切线的性质直角三角形的性质求⊙O的半径

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 论是否仍然成立?请说明理由;
论是否仍然成立?请说明理由;
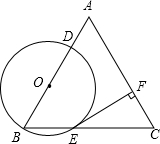 已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.