题目内容
如图，BE、CF是△ABC的角平分线，且∠A=70°，那么∠BDC的度数是
- A.70°
- B.115°
- C.125°
- D.145°
C
分析：根据三角形的内角和定理和∠A的度数求得另外两个内角的和，利用角平分线的性质得到这两个角和的一半，用三角形内角和减去这两个角的一半即可．
解答：∵∠A=70°，
∴∠ABC+∠ACB=180°-∠A=180°-70°=110°，
∵BE、CF是△ABC的角平分线，
∴∠EBC+∠FCB=
（∠ABC+∠ACB）=55°，
∴∠BDC=180°-55°=125°．
故选C．
点评：本题考查了三角形的内角和定理，此定理对学生来说比较熟悉，但有时运用起来却不很熟练，难度较小．
分析：根据三角形的内角和定理和∠A的度数求得另外两个内角的和，利用角平分线的性质得到这两个角和的一半，用三角形内角和减去这两个角的一半即可．
解答：∵∠A=70°，
∴∠ABC+∠ACB=180°-∠A=180°-70°=110°，
∵BE、CF是△ABC的角平分线，
∴∠EBC+∠FCB=
（∠ABC+∠ACB）=55°，∴∠BDC=180°-55°=125°．
故选C．
点评：本题考查了三角形的内角和定理，此定理对学生来说比较熟悉，但有时运用起来却不很熟练，难度较小．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
如图，BE、CF是△ABC的角平分线，∠A=50°，则∠BOC的度数是（ ）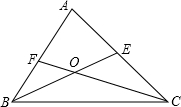
| A、50° | B、65° | C、115° | D、110° |
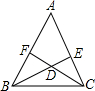如图，BE，CF是△ABC的角平分线，∠A=65°，那么BDC等于（ ）| A、122.5° | B、187.5° | C、178.5° | D、115° |
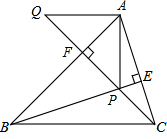如图，BE、CF是△ABC的高，且BP=AC，CQ=AB．求证：AP⊥AQ．
如图，BE、CF是△ABC的角平分线，∠ABC=80°，∠ACB=60°，BE、CF相交于D，则∠CDE的度数是（ ）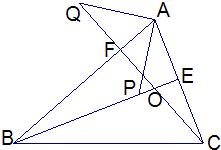
如图，BE、CF是△ABC的高，它们相交于点O，点P在BE上，Q在CF的延长线上且BP=AC，CQ=AB，