Question

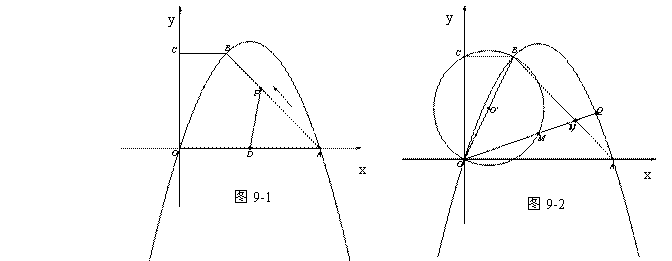
已知：如图9-1，抛物线经过点O、A、B三点，四边形OABC是直角梯形，其中点A在x轴上，点C在y轴上，BC∥OA，A（12，0）、B（4，8）．

（1）求抛物线所对应的函数关系式；（3分）

（2）若D为OA的中点，动点P自A点出发沿A→B→C→O的路线移动，速度为每秒1个单位，移动时间记为t秒．几秒钟后线段PD将梯形OABC的面积分成

1﹕3两部分？并求出此时P点的坐标；（3分）

（3）如图9-2，作△OBC的外接圆O′，点Q是抛物线上点A、B之间的动点，连接OQ交⊙O′于点M，交AB于点N．当∠BOQ=45°时，求线段MN的长．（3分）

 

Answer 1

（1）解：∵抛物线经过O（0，0）、A（12，0）、B（4，8）

∴设抛物线的解析式为：

∴将点B的坐标代入，得：，解得：，

∴所求抛物线的关系式为：

（2）解：过点B作BF⊥x轴于点F，∵BF=8，AF=12-4=8∴∠BAF = 45º

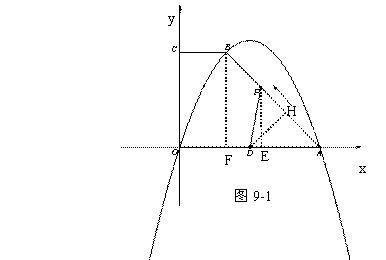
∴S_梯形OABC= ∴面积分成1﹕3两部分，即面积分成16﹕48

由题意得，动点P整个运动过程分三种情况，但点P在BC上时，

由于∵S_△ABD= ∴点P在BC上不能满足要求。…

即点P只能在AB或OC上才能满足要求，

① 点P在AB上，设P(x,y)

可得S_△APD=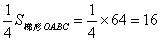

又S_△APD=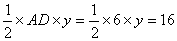

∴ y=

过P作PE⊥x轴于点E,由∠BAF = 45º

∴AE=PE=

∴x=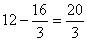

又过D作DH⊥AB于H,

∵AD=6

∴DH=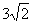

∵S_△APD=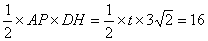

∴t=

∴当t=时，P满足要求。

② 点P在OC上，设P(0,y)

∵S_△APD=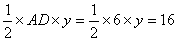

∴ y= ∴P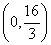

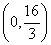∴此时t=AB+BC+CP=, P满足要求。

（3）解：连接BM， ∵OB是圆直径，

∴BM⊥OＭ，

∵BC=4，OC=8

∴OB=

∵ 在Rt△BMO中∠BOQ=45°

∴OM=

由（2）可知：∠OAB=45°,AB=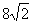

∵∠BOQ=45°

∴∠BOA=∠BOQ+∠AON =45°+∠AON

又∵∠BNO=45°+∠AON

∴∠BNO =∠BOA

又∵∠BON=∠BAO=45°

∴△BON∽△BAO

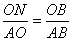∴ 即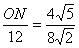

∴ON=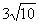

∴MN=ON-OM=