题目内容
如图,已知在⊙O中,AB=4 ,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
(1)求图中阴影部分的面积;
|
(1)

(2)
 解析:
解析:解:(1)法一:过O作OE⊥AB于E,则AE=
 AB=2
AB=2 . 1分
. 1分 在Rt
在Rt AEO中,∠BAC=30°,cos30°=
AEO中,∠BAC=30°,cos30°= .
.∴OA=
 =
= =4. …………………………3分
=4. …………………………3分又∵OA=OB,∴∠ABO=30°.∴∠BOC=60°.
∵AC⊥BD,∴
 .
.∴∠COD =∠BOC=60°.∴∠BOD=120°. 5分
∴S阴影=
 =
= . 6分
. 6分法二:连结AD. 1分
∵AC⊥BD,AC是直径,

|
 .
. ∴∠BAD=2∠BAC=60°,
∴∠BOD=120°. ……………………3分
∵BF=
 AB=2
AB=2 ,sin60°=
,sin60°= ,
,AF=AB·sin60°=4
 ×
× =6.
=6.∴OB2=BF2+OF2.即
 .
.∴OB=4. 5分
∴S阴影=
 S圆=
S圆= . 6分
. 6分法三:连结BC.………………………………………………………………………………1分
∵AC为⊙O的直径, ∴∠ABC=90°.
 ∵AB=4
∵AB=4 ,
,∴
 . ……………………3分
. ……………………3分∵∠A=30°, AC⊥BD, ∴∠BOC=60°,
∴∠BOD=120°.
∴S阴影=
 π·OA2=
π·OA2= ×42·π=
×42·π= .……………………6分
.……………………6分以下同法一.
(2)设圆锥的底面圆的半径为r,则周长为2πr,
∴
 .
. ∴
 . 10分
. 10分 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 20、如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
20、如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.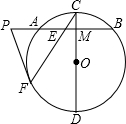 作⊙O的切线交BA的延长线于点P.
作⊙O的切线交BA的延长线于点P. (2011•普宁市一模)如图,已知在?ABCD中,E、F是对角线BD延长线上的两点,且∠BCE=∠DAF,求证:△ECD≌△FAB.
(2011•普宁市一模)如图,已知在?ABCD中,E、F是对角线BD延长线上的两点,且∠BCE=∠DAF,求证:△ECD≌△FAB. 如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数.
如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数.