题目内容
如图，已知在⊙O中，CD是直径，弦AB⊥CD，M是垂足，E为MA上的一点，连接C、E两点并延长交⊙O于F，过F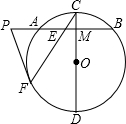
作⊙O的切线交BA的延长线于点P．求证：CE•EF=2PE•EM．
分析：从求证式看，关键是数字2，观察图形，发现直径是半径的2倍，再从已知出发，连接OF、FD，
由△PEF∽△ODF，得出
=
，由△CEM∽△CDF，得出
=
，
再将两式相除，把CD=2OF代入即可求出．
由△PEF∽△ODF，得出
| PE |
| OF |
| EF |
| DF |
| CE |
| CD |
| EM |
| DF |
再将两式相除，把CD=2OF代入即可求出．
解答：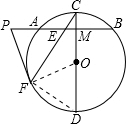
证明：连接0F、FD，
?
?
=
?CE•EF=2PE•EM
证明：连接0F、FD，
|
?
|
?
| 2PE |
| CE |
| EF |
| EM |
?CE•EF=2PE•EM
点评：本题考查相似三角形的判定及性质，有一定难度，关键是对数字2的处理．
练习册系列答案
相关题目
20、如图：已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F．
（2011•普宁市一模）如图，已知在?ABCD中，E、F是对角线BD延长线上的两点，且∠BCE=∠DAF，求证：△ECD≌△FAB．
如图，已知在△ABC中，AB=AC，AB的垂直平分线DE交AC于点E，CE的垂直平分线正好经过点B，与AC相交于点F，求∠A的度数．